Lời giải chi tiết:

Ta có \(f'\left( x \right) = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 1 - {m^2} = g\left( x \right)\).

Để hàm số  \(\)\(y = f\left( {\left| x \right|} \right)\) có số điểm cực trị lớn hơn 5 thì phương trình \(f'\left( x \right) = 0\) có 3 nghiệm dương phân biệt.

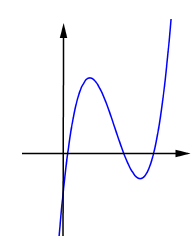
\(y = g\left( x \right)\) là hàm đa thức bậc ba có hệ số \(a = 1 > 0\), để phương trình \(g\left( x \right) = 0\) có 3 nghiệm dương phân biệt thì đồ thị hàm số có dạng như sau:

Khi đó hàm số phải thỏa mãn các điều kiện sau:

+) \(g\left( 0 \right) < 0\) (1).

+) Hàm số \(g\left( x \right) = 0\) có 2 điểm cực trị \({x_1};\,{x_2}\)  cùng dấu dương (2).

+) \(g\left( {{x_1}} \right)g\left( {{x_2}} \right) < 0\) (3).

Giải (1): \(g\left( 0 \right) < 0 \Leftrightarrow 1 - {m^2} < 0 \Leftrightarrow \left[ \begin{array}{l}m > 1\\m <  - 1\end{array} \right.\).

Giải (2):

Ta có phương trình \(g'\left( x \right) = 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right) = 0 \Leftrightarrow {x^2} - 2mx + {m^2} - 1 = 0\).

Ta có: \(\Delta ' = {m^2} - {m^2} + 1 = 1 \Leftrightarrow \left[ \begin{array}{l}{x_1} = m + 1\\{x_2} = m - 1\end{array} \right.\)

Hàm số \(g\left( x \right) = 0\) có 2 điểm cực trị cùng dấu dương suy ra phương trình \(g'\left( x \right) = 0\) có 2 nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}m + 1 > 0\\m - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m >  - 1\\m > 1\end{array} \right. \Leftrightarrow m > 1\).

Giải (3):

\(\begin{array}{l}{x_1} = m + 1 \Rightarrow g\left( {{x_1}} \right) = {\left( {m + 1} \right)^3} - 3m{\left( {m + 1} \right)^2} + 3\left( {{m^2} - 1} \right)\left( {m + 1} \right) - {m^2} = {m^3} - {m^2} - 3m - 1\\{x_2} = m - 1 \Rightarrow g\left( {{x_2}} \right) = {\left( {m - 1} \right)^3} - 3m{\left( {m - 1} \right)^2} + 3\left( {{m^2} - 1} \right)\left( {m - 1} \right) - {m^2} = {m^3} - {m^2} - 3m + 3\end{array}\)

\(\begin{array}{l}\left( 3 \right) \Leftrightarrow \left( {{m^3} - {m^2} - 3m - 1} \right)\left( {{m^3} - {m^2} - 3m + 3} \right) < 0\\ \Leftrightarrow  - 3 < {m^3} - {m^2} - 3m < 1 \Leftrightarrow \left[ \begin{array}{l} - \sqrt 3  < m <  - 1\\1 - \sqrt 2  < m < 1\end{array} \right.\\ \Leftrightarrow \sqrt 3  < m < 1 + \sqrt 2  \Leftrightarrow 3 < {m^2} < 3 + 2\sqrt 2 \\ \Rightarrow \left\{ \begin{array}{l}a = 3\\b = 3\\c = 2\end{array} \right. \Rightarrow T = a + b + c = 8\end{array}\)

Chọn B.