Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ. Số điểm cực trị của hàm số \(y = f\left( {x - 2017} \right) - 2018x + 2019\) là:
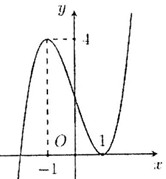
- A 1
- B 3
- C 2
- D 0
Phương pháp giải:
Xác định số điểm mà \(y'\) đổi dấu.
Lời giải chi tiết:
Ta có: \(y = f\left( {x - 2017} \right) - 2018x + 2019 \Rightarrow y' = f'\left( {x - 2017} \right) - 2018\)
\(y' = 0 \Leftrightarrow f'\left( {x - 2017} \right) = 2018 \Leftrightarrow x - 2017 = {x_0} \Leftrightarrow x = 2017 + {x_0}\), với \({x_0} > 1\) và là duy nhất.
Do đó, \(y'\) đổi dấu tại duy nhất 1 điểm \( \Rightarrow \)Hàm số \(y = f\left( {x - 2017} \right) - 2018x + 2019\) có duy nhất 1 cực trị.
Chọn: A
Câu hỏi trước
