Câu hỏi
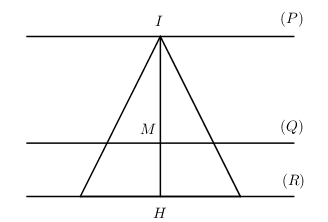
Trong không gian Oxyz, cho hình nón có đỉnh \(I\) thuộc mặt phẳng \((P):2x - y - 2z - 7 = 0\) và hình tròn đáy nằm trên mặt phẳng \((R):2x - y - 2z + 8 = 0\). Mặt phẳng \((Q)\) đi qua điểm \(A(0; - 2;0)\) và vuông góc với trục của hình nón chia hình nón thành hai phần có thể tích lần lượt là \({V_1}\;\)và \({V_2}\) ( \({V_1}\) là thể tích của phần chứa đỉnh \(I\)). Biết rằng biểu thức \(S = {V_2} + \dfrac{{78}}{{V_1^3}}\) đạt giá trị nhỏ nhất khi \({V_1} = a,\;\;{V_2} = b.\;\)Khi đó tổng \({a^2} + {b^2}\) bằng
- A \(2031{\pi ^2}.\)
- B \(377\sqrt 3 .\)
- C \(52\sqrt 3 {\pi ^2}.\)
- D \(2031.\)
Lời giải chi tiết:
Dễ thấy \(\left( P \right)//\left( R \right)\) , do đó \(IH = d\left( {\left( P \right);\left( Q \right)} \right)\).
Lấy \(B\left( {0; - 7;0} \right) \in \left( P \right) \Rightarrow d\left( {\left( P \right);\left( R \right)} \right) = d\left( {B;\left( R \right)} \right) = \dfrac{{\left| {2.0 - \left( { - 7} \right) - 2.0 + 8 = 0} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = 5\).
\( \Rightarrow IH = 5\).
Mặt phẳng \((Q)\) đi qua điểm \(A(0; - 2;0)\) và vuông góc với trục của hình nón \( \Rightarrow \left( Q \right)//\left( P \right)\).
\( \Rightarrow \left( Q \right):\,\,2x - y - 2z - 2 = 0\).
\(d\left( {B;\left( Q \right)} \right) = \dfrac{{\left| {2.0 - \left( { - 7} \right) - 2.0 - 2} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = \dfrac{5}{3} = IM\).
Gọi \({R_1};R\) lần lượt là bán kính của hình nón có thể tích \({V_1}\) và khối nón to.
Áp dụng định lí Ta-lét ta có: \(\dfrac{{{R_1}}}{R} = \dfrac{{IM}}{{IH}} = \dfrac{{\dfrac{5}{3}}}{5} = \dfrac{1}{3}\)
\( \Rightarrow \dfrac{{{V_1}}}{V} = \dfrac{{\dfrac{1}{3}\pi R_1^2.IM}}{{\dfrac{1}{3}\pi {R^2}.IH}} = {\left( {\dfrac{1}{3}} \right)^2}.\dfrac{1}{3} = \dfrac{1}{{27}} \Rightarrow {V_1} = \dfrac{V}{{27}} \Rightarrow {V_2} = 26{V_1}\).
Ta có: \(S = {V_2} + \dfrac{{78}}{{V_1^3}} = 26{V_1} + \dfrac{{78}}{{V_1^3}} = \dfrac{{26{V_1}}}{3} + \dfrac{{26{V_1}}}{3} + \dfrac{{26{V_1}}}{3} + \dfrac{{78}}{{V_1^3}} \ge 4\sqrt[4]{{\dfrac{{{{26}^3}.78}}{{{3^3}}}}} = \dfrac{{104\sqrt 3 }}{3}\).
Dấu “=” xảy ra \( \Leftrightarrow \dfrac{{26{V_1}}}{3} = \dfrac{{78}}{{V_1^3}} \Leftrightarrow V_1^4 = 9 \Leftrightarrow {V_1} = \sqrt 3 = a;\,\,{V_2} = 26\sqrt 3 = b\)
\( \Rightarrow {a^2} + {b^2} = {\left( {\sqrt 3 } \right)^2} + {\left( {26\sqrt 3 } \right)^2} = 2031\).
Chọn D.