Phương pháp giải:

\(d\left( {B;\left( {SAC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SAC}}}}\)

Lời giải chi tiết:

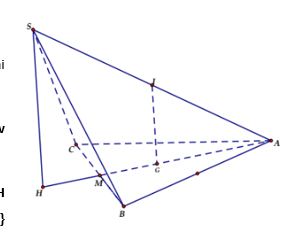
Gọi \(I\) là trung điểm của \(SA\).

Tam giác \(SAB,\,\,SAC\) là các tam giác vuông tại \(B,\,C \Rightarrow IS = IA = IB = IC\).

Gọi \(G\) là trọng tâm tam giác đều \(ABC \Rightarrow IG \bot \left( {ABC} \right)\).

Trong \(\left( {SAG} \right)\) kẻ \(SH//IG\,\,\left( {H \in CG} \right) \Rightarrow SH \bot \left( {ABC} \right)\). Dễ thấy khi đó \(IG\) là đường trung bình của tam giác \(SAH \Rightarrow SH = 2IG\).

Tam giác \(ABC\) đều cạnh \(2a \Rightarrow AG = \dfrac{2}{3}\dfrac{{2a\sqrt 3 }}{2} = \dfrac{{2a\sqrt 3 }}{3}\).

Ta có \(\angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;AH} \right) = \angle SAH = {45^0}\).

\( \Rightarrow \Delta AIG\) vuông cân tại \(G \Leftrightarrow IG = AG = \dfrac{{2a\sqrt 3 }}{3} \Rightarrow SH = 2IG = \dfrac{{4a\sqrt 3 }}{3}\).

\( \Rightarrow {V_{S.ABC}} = \dfrac{1}{3}SH.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{4a\sqrt 3 }}{3}\dfrac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = \dfrac{{4{a^3}}}{3}\).

Ta có \(GA = GB = GC\); \(GA = GH\) (\(IG\) là đường trung bình của tam giác \(SAH\))

\( \Rightarrow GA = GB = GC = GH \Rightarrow G\) là tâm đường tròn ngoại tiếp tứ giác \(ABHC\).

\( \Rightarrow AH\) là đường kính đường tròn ngoại tiếp tứ giác \(ABHC\).

\( \Leftrightarrow \angle ACH = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

Ta có: \(AH = 2AG = \dfrac{{4a\sqrt 3 }}{3} \Rightarrow CH = \sqrt {A{H^2} - A{C^2}}  = \dfrac{{2a}}{{\sqrt 3 }}\).

\( \Rightarrow SC = \sqrt {S{H^2} + H{C^2}}  = \sqrt {{{\left( {\dfrac{{4a\sqrt 3 }}{3}} \right)}^2} + {{\left( {\dfrac{{2a}}{{\sqrt 3 }}} \right)}^2}}  = \dfrac{{2\sqrt {15} a}}{3}\).

\({S_{\Delta SAC}} = \dfrac{1}{2}SC.AC = \dfrac{1}{2}.\dfrac{{2\sqrt {15} a}}{3}.2a = \dfrac{{2\sqrt {15} {a^2}}}{3}\).

Vậy \(d\left( {B;\left( {SAC} \right)} \right) = \dfrac{{3{V_{S.ABC}}}}{{{S_{\Delta SAC}}}} = \dfrac{{3.\dfrac{{4{a^3}}}{3}}}{{\dfrac{{2\sqrt {15} {a^2}}}{3}}} = \dfrac{{2a\sqrt {15} }}{5}\).

Chọn B.