Phương pháp giải:

Đường trung trực của đoạn thẳng \(AB\) đi qua trung điểm \(I\) của \(AB\) và nhận vecto \(\overrightarrow {AB} \) làm VTPT.

Lời giải chi tiết:

Gọi I là trung điểm của AB \( \Rightarrow I\left( {\frac{5}{2};\frac{3}{2}} \right)\)

Gọi \(\Delta \) là đường trung trực của AB \( \Rightarrow I \in \Delta \)

\(\overrightarrow {AB}  = \left( {3; - 1} \right)\) là một VTPT của \(\Delta \)

\( \Rightarrow \Delta :3\left( {x - \frac{5}{2}} \right) - \left( {y - \frac{3}{2}} \right) = 0 \Leftrightarrow 3x - y - 6 = 0\)

Chọn B.

Phương pháp giải:

Gọi \(M\left( {m;2m - 5} \right) \in d\) là tâm của đường tròn \(\left( C \right)\), lập phương trình tìm \(m.\)

Lời giải chi tiết:

Gọi \(M\left( {m;2m - 5} \right) \in d\) là tâm của đường tròn \(\left( C \right)\)

Đường tròn \(\left( C \right)\) đi qua \(A,\,\,B \Rightarrow MA = MB \Leftrightarrow M{A^2} = M{B^2}\)

\(\begin{array}{l} \Leftrightarrow {\left( {1 - m} \right)^2} + {\left( {2 - 2m + 5} \right)^2} = {\left( {4 - m} \right)^2} + {\left( {1 - 2m + 5} \right)^2}\\ \Leftrightarrow {\left( {1 - m} \right)^2} - {\left( {4 - m} \right)^2} = {\left( {6 - 2m} \right)^2} - {\left( {7 - 2m} \right)^2}\\ \Leftrightarrow  - 3\left( {5 - 2m} \right) =  - \left( {13 - 4m} \right) \Leftrightarrow 2m = 2 \Leftrightarrow m = 1\\ \Rightarrow M\left( {1; - 3} \right)\end{array}\) 

Bán kính của đường tròn \(\left( C \right)\) là \(MA = \sqrt {0 + {5^2}}  = 5\)

\( \Rightarrow \) Phương trình đường tròn \(\left( C \right)\): \({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 25.\)

Chọn D.

Phương pháp giải:

Viết phương trình đường thẳng qua tâm M song song với đường thẳng d’ từ đó tìm giao của đường thẳng với đường tròn. Hai điểm đó chính là tiếp điểm của hai tiếp tuyến cần tìm.

Lời giải chi tiết:

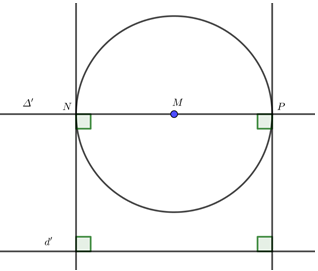
Gọi \(\Delta '\) là đường thẳng qua M song song với d’

\( \Rightarrow \overrightarrow n  = \left( {1;1} \right)\) là VTPT của d’ và  \(\Delta '\)

\( \Rightarrow \Delta ':\left( {x - 1} \right) + \left( {y + 3} \right) = 0 \Leftrightarrow x + y + 2 = 0\)

Gọi \(N,\,\,P\) là giao điểm của \(\Delta '\) với \(\left( C \right)\)

\( \Rightarrow \) Tọa độ \(N,\,\,P\) là nghiệm của hệ:

\(\begin{array}{l}\left\{ \begin{array}{l}x + y + 2 = 0\\{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 25\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - y - 2\\{\left( { - y - 3} \right)^2} + {\left( {y + 3} \right)^2} = 25\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - y - 2\\{\left( {y + 3} \right)^2} = \frac{{25}}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1 - \frac{5}{{\sqrt 2 }}\\y = \frac{5}{{\sqrt 2 }} - 3\end{array} \right. \Rightarrow N\left( {1 - \frac{5}{{\sqrt 2 }};\frac{5}{{\sqrt 2 }} - 3} \right)\\\left\{ \begin{array}{l}x = 1 + \frac{5}{{\sqrt 2 }}\\y =  - \frac{5}{{\sqrt 2 }} - 3\end{array} \right. \Rightarrow P\left( {1 + \frac{5}{{\sqrt 2 }}; - \frac{5}{{\sqrt 2 }} - 3} \right)\end{array} \right.\end{array}\) Vì tiếp tuyến cần tìm vuông góc với d’ nên chúng cũng vuông góc với \(\Delta '\)

\( \Rightarrow \) Các tiếp tuyến cần tìm tiếp xúc với đương tròn \(\left( C \right)\) tại \(N,\,\,P\)

\(\overrightarrow {n'}  = \left( {1; - 1} \right)\) là VTPT của các tiếp tuyến cần tìm

+) Với tiếp điểm N

\( \Rightarrow \) Phương trình tiếp tuyến \({d_1}:\left( {x - 1 + \frac{5}{{\sqrt 2 }}} \right) - y + \frac{5}{{\sqrt 2 }} - 3 = 0 \Leftrightarrow x - y + \frac{{10}}{{\sqrt 2 }} - 4 = 0\)

+) Với tiếp điểm P

\( \Rightarrow \) Phương trình tiếp tuyến \({d_2}:\left( {x - 1 - \frac{5}{{\sqrt 2 }}} \right) - y - \frac{5}{{\sqrt 2 }} - 3 = 0 \Leftrightarrow x - y - \frac{{10}}{{\sqrt 2 }} - 4 = 0\)

Vậy có hai phương trình tiếp tuyến thỏa mãn bài toán: \(\left[ \begin{array}{l}x - y + \frac{{10}}{{\sqrt 2 }} - 4 = 0\\x - y - \frac{{10}}{{\sqrt 2 }} - 4 = 0\end{array} \right..\)

Chọn A.