Phương pháp giải:

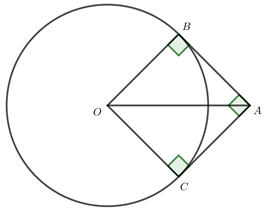
Chứng minh ABOC là hình vuông từ đó tính OA để suy ra \(m.\)

Lời giải chi tiết:

Từ A kẻ 2 tiếp tuyến \(AB,\,\,AC\)  với \(\left( C \right)\)

\(\left( C \right)\) có tâm \(O\left( {2; - 1} \right)\) bán kính \(R = 1\)

Tứ giác ABOC có \(\left\{ \begin{array}{l}\angle A = \angle B = \angle C = {90^o}\\OB = OC = R\end{array} \right.\)

\( \Rightarrow \) ABOC là hình vuông (dhnb).

\( \Rightarrow AC = OC = R = 1 \Rightarrow OA = \sqrt 2 \)

\(\begin{array}{l} \Leftrightarrow \sqrt {{{\left( {m - 2} \right)}^2} + {{\left( {1 - m + 1} \right)}^2}}  = \sqrt 2  \Leftrightarrow 2{\left( {m - 2} \right)^2} = 2 \Leftrightarrow {\left( {m - 2} \right)^2} = 1\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 1\\m - 2 =  - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 3\\m = 1\end{array} \right.\end{array}\) 

Chọn A.