Phương pháp giải:

Hàm số \(y = f\left( x \right)\) đồng biến trên \(\mathbb{R} \Leftrightarrow f'\left( x \right) \ge 0\,\,\forall x \in \mathbb{R}\) và \(f'\left( x \right) = 0\) tại hữu hạn điểm.

Lời giải chi tiết:

Ta có: \(y = x + m\sqrt {{x^2} + 2} \)\( \Rightarrow y' = 1 + \dfrac{{mx}}{{\sqrt {{x^2} + 2} }}.\)

Hàm số đã cho đồng biến trên \(\mathbb{R} \Leftrightarrow y' \ge 0\,\,\forall x \in \mathbb{R}\) và bằng 0 tại hữu hạn điểm.

\(\begin{align} \Leftrightarrow 1+\dfrac{mx}{\sqrt{{{x}^{2}}+2}}\ge 0\,\,\forall x\in \mathbb{R}\Leftrightarrow \sqrt{{{x}^{2}}+2}+mx\ge 0\,\forall x\in \mathbb{R} \\ \Leftrightarrow mx\ge -\sqrt{{{x}^{2}}+2}\,\forall x\in \mathbb{R}\,\,\,\,\left( * \right) \\ \end{align}\)

+) Với \(x=0\Rightarrow y'\ge 0\,\,\,\forall m\Rightarrow tm\).

+) Với \(x>0\) ta có: \(\left( * \right)\Leftrightarrow m\ge -\dfrac{\sqrt{{{x}^{2}}+2}}{x}=g\left( x \right)\,\,\forall x\in \mathbb{R}\Leftrightarrow m\ge \underset{\left( 0;+\infty  \right)}{\mathop{\max }}\,g\left( x \right)\).

+) Với \(x < 0\) ta có: \(\left( * \right)\Leftrightarrow m\le -\dfrac{\sqrt{{{x}^{2}}+2}}{x}=g\left( x \right)\,\,\forall x\in \mathbb{R}\Leftrightarrow m\le \underset{\left( -\infty ;\,\,0 \right)}{\mathop{\min }}\,g\left( x \right)\)

Xét \(g\left( x \right)=-\dfrac{\sqrt{{{x}^{2}}+2}}{x}\,\,\left( x\ne 0 \right)\) ta có:

\(g'\left( x \right)=\dfrac{-\dfrac{x}{\sqrt{{{x}^{2}}+2}}x+\sqrt{{{x}^{2}}+2}}{{{x}^{2}}}=\dfrac{-{{x}^{2}}+{{x}^{2}}+2}{{{x}^{2}}\sqrt{{{x}^{2}}+2}}=\dfrac{2}{{{x}^{2}}\left( {{x}^{2}}+2 \right)}>0\,\,\forall x\in \mathbb{R}\)

 Hàm số đồng biến trên trên \(\left( -\infty ;0 \right)\) và \(\left( 0;+\infty  \right)\).

BBT:

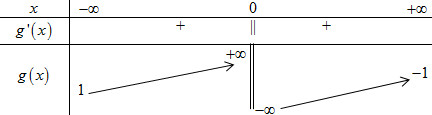
Dựa vào BBT ta có: \( - 1 \le m \le 1\) thỏa mãn bài toán. Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 1;\,0;\,1} \right\}.\)

Chọn D.