Câu hỏi
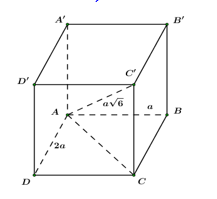
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = a,\,\,AD = 2a,\,AC' = \sqrt 6 a.\) Thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\) bằng:
- A \(\dfrac{{\sqrt 3 {a^3}}}{3}\)
- B \(\dfrac{{2{a^3}}}{3}\)
- C \(2{a^3}\)
- D \(2\sqrt 3 {a^3}\)
Phương pháp giải:
Công thức tính thể tích khối hộp chữ nhật \(ABCD.A'B'C'D'\) là: \(V = AA'.AB.AD.\)
Lời giải chi tiết:
Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \) (định lý Pitago)
Xét tam giác \(ACC'\) vuông tại \(C\) ta có:
\(\begin{array}{l}CC' = \sqrt {AC{'^2} - A{C^2}} = \sqrt {6{a^2} - 5{a^2}} = a.\\ \Rightarrow {V_{ABCD.A'B'C'D'}} = CC'.AB.AD = a.a.2a = 2{a^3}.\end{array}\)
Chọn C.
Câu hỏi trước
