Lời giải chi tiết:

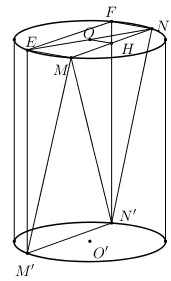
Gọi \(O,\,\,O'\) lần lượt là tâm 2 đáy chứa \(MN,\,\,M'N'\).

Gọi \(E,\,\,F\) lần lượt là hình chiếu của \(M',\,N'\) lên đường tròn \(\left( O \right)\).

Khi đó \(EFN'M'\) là hình chữ nhật \(\left\{ \begin{array}{l}EF//M'N'\\EF = M'N' = 6\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}EF//MN\\EF = MN = 6\end{array} \right. \Rightarrow EFNM\) là hình bình hành. Mà \(EFNM\) nội tiếp \(\left( O \right) \Rightarrow EFNM\) là hình chữ nhật.

\( \Rightarrow \angle EMN = {90^0} \Rightarrow \angle EMN\) chắn nửa đường tròn \( \Rightarrow E,O,N\) thẳng hàng.

Ta có: \(\left\{ \begin{array}{l}MN \bot EM\\MN \bot M'E\end{array} \right. \Rightarrow MN \bot \left( {M'ME} \right) \Rightarrow MN \bot MM'\)

\( \Rightarrow {S_{MNN'M'}} = MM'.MN \Leftrightarrow 60 = MM'.6 \Leftrightarrow MM' = 10\)

Gọi \(H\) là trung điểm của \(MN \Rightarrow OH \bot MN\).

Có \(EM \bot MN \Rightarrow EM//OH\).

\( \Rightarrow OH\) là đường trung bình của tam giác \(EMN\).

Xét tam giác vuông \(OHN:\,\,OH = \sqrt {O{N^2} - H{N^2}}  = \sqrt {{4^2} - {3^2}}  = \sqrt 7 \)\( \Rightarrow EM = 2OH = 2\sqrt 7 \).

Xét tam giác vuông \(MM'E:\,\,M'E = \sqrt {MM{'^2} - E{M^2}}  = \sqrt {{{10}^2} - {{\left( {2\sqrt 7 } \right)}^2}}  = 6\sqrt 2  = h\).

Chọn D.