Câu hỏi
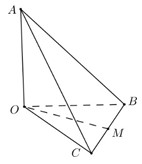
Cho tứ diện \(OABC\) có \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau và \(OA = OB = OC = 1\). Gọi \(M\) là trung điểm của \(BC\) (tham khảo hình vẽ bên). Góc giữa hai đường thẳng \(OM\) và \(AB\) bằng:
- A \({90^0}\)
- B \({30^0}\)
- C \({60^0}\)
- D \({45^0}\)
Phương pháp giải:
Gọi \(N\) là trung điểm của \(AC \Rightarrow MN\) là đường trung bình của tam giác
\( \Rightarrow MN//AB\)\( \Rightarrow \angle \left( {OM;AB} \right) = \angle \left( {OM;MN} \right)\).
Lời giải chi tiết:
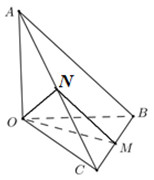
Gọi \(N\) là trung điểm của \(AC \Rightarrow MN\) là đường trung bình của tam giác
\( \Rightarrow MN//AB\)\( \Rightarrow \angle \left( {OM;AB} \right) = \angle \left( {OM;MN} \right)\).
Trong tam giác vuông \(OBC\) có \(OM = \dfrac{1}{2}BC = \dfrac{{\sqrt 2 }}{2}\).
Trong tam giác vuông \(OAC\) có \(ON = \dfrac{1}{2}AC = \dfrac{{\sqrt 2 }}{2}\).
Trong tam giác vuông \(OAB\) có \(MN = \dfrac{1}{2}AB = \dfrac{{\sqrt 2 }}{2}\).
\( \Rightarrow OM = ON = MN = \dfrac{{\sqrt 2 }}{2} \Rightarrow \Delta OMN\) đều \( \Rightarrow \angle OMN = {60^0}\).
Vậy \(\angle \left( {OM;AB} \right) = {60^0}\).
Chọn C.







