Câu hỏi
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Tích vô hướng của hai véctơ \(\overrightarrow {AB} \) và \(\overrightarrow {A'C'} \) bằng :
- A \({a^2}\sqrt 2 \)
- B \({a^2}\dfrac{{\sqrt 2 }}{2}\)
- C \({a^2}\)
- D \(0\)
Phương pháp giải:
Sử dụng công thức \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \angle \left( {\overrightarrow a ;\overrightarrow b } \right)\).
Lời giải chi tiết:
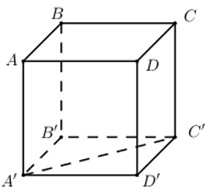
Ta có:
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {A'C'} = AB.A'C'.\cos \angle \left( {\overrightarrow {AB} ;\overrightarrow {A'C'} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = AB.A'C'.\cos \angle \left( {\overrightarrow {A'B'} ;\overrightarrow {A'C'} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = a.a\sqrt 2 .\cos {45^0} = {a^2}\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = {a^2}\end{array}\)
Chọn C.
Câu hỏi trước
