Câu hỏi
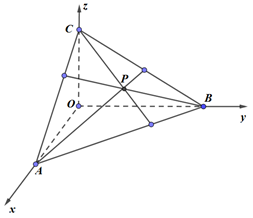
Trong không gian với hệ tọa độ Oxyz, cho điểm \(P\left( {1;2;2} \right)\). Mặt phẳng \(\left( \alpha \right)\) đi qua P cắt các tia \(Ox,Oy,Oz\) tại \(A,B,C\) khác gốc tọa độ sao cho \(T = \frac{{R_1^2}}{{S_1^2}} + \frac{{R_2^2}}{{S_2^2}} + \frac{{R_3^2}}{{S_3^2}}\) đạt giá trị nhỏ nhất, trong đó \({S_1},{S_2},{S_3}\) lần lượt là diện tích \(\Delta OAB,\,\Delta OBC,\,\Delta OCA\) và \({R_1},{R_2},{R_3}\) lần lượt là diện tích các tam giác \(\Delta PAB,\Delta PBC,\Delta PCA\). Khi đó, điểm M nào sau đây thuộc mặt phẳng \(\left( \alpha \right)\)?
- A \(M\left( {5;0;2} \right)\).
- B \(M\left( {2;1;5} \right)\).
- C \(M\left( {2;1;2} \right)\).
- D \(M\left( {2;0;5} \right)\).
Phương pháp giải:
Sử dụng tính chất của tứ diện vuông: \(S_{\Delta BAC}^2 = S_{\Delta OAC}^2 + S_{\Delta BOC}^2 + S_{\Delta BAO}^2\) và bất đẳng thức: \(\frac{{{a^2}}}{x} + \frac{{{b^2}}}{y} + \frac{{{c^2}}}{z} \ge \frac{{{{\left( {a + b + c} \right)}^2}}}{{x + y + z}}\)
(dấu “=” xảy ra khi và chỉ khi \(\frac{a}{x} = \frac{b}{y} = \frac{c}{z}\)) .
Lời giải chi tiết:
Ta có: \(T = \frac{{R_1^2}}{{S_1^2}} + \frac{{R_2^2}}{{S_2^2}} + \frac{{R_3^2}}{{S_3^2}} \ge \frac{{{{\left( {{R_1} + {R_2} + {R_3}} \right)}^2}}}{{S_1^2 + S_2^2 + S_3^2}} = \frac{{S_{\Delta ABC}^2}}{{S_{\Delta ABC}^2}} = 1\)
Dấu “=” xảy ra khi và chỉ khi : \(\frac{{R_1^{}}}{{S_1^2}} = \frac{{R_2^{}}}{{S_2^2}} = \frac{{R_3^{}}}{{S_3^2}} \Leftrightarrow \) P là hình chiếu vuông góc của O lên \(\left( \alpha \right)\)
\( \Leftrightarrow \)\(\left( \alpha \right)\) là mặt phẳng qua \(P\left( {1;2;2} \right)\), nhận \(\overrightarrow {OP} = \left( {1;2;2} \right)\) làm VTPT, có phương trình là:
\(1\left( {x - 1} \right) + 2\left( {y - 2} \right) + 2\left( {z - 2} \right) = 0 \Leftrightarrow x + 2y + 2z - 9 = 0\)
Vậy, \({T_{\min }} = 1\) khi và chỉ khi \(\left( \alpha \right):x + 2y + 2z - 9 = 0\)
Dễ dàng kiểm tra được: \(M\left( {5;0;2} \right) \in \left( \alpha \right)\).
Chọn: A