Câu hỏi
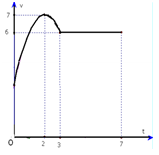
Một vật chuyển động trong 7 giờ với vận tốc \(v\,\,\left( {km/h} \right)\) phụ thuộc vào thời gian \(t\,\left( h \right)\) có đồ thị của vận tốc như hình dưới đây. Trong khoảng thời gian 3 giờ kể từ bắt đầu chuyển động, đồ thị là phần Parabol có đỉnh \(I\left( {2;7} \right)\), trục đối xứng song song với trục tung, khoảng thời gian còn lại đồ thị là đoạn thẳng song song trục hoành. Tính quãng đường \(S\) mà vật di chuyển trong 7 giờ đó.
- A \(S = 48\,km\).
- B \(S = 42\,km\).
- C \(S = 40\,km\).
- D \(S = 36\,km\).
Phương pháp giải:
- Lập hàm vận tốc trên đoạn từ \(\left[ {0;7} \right],\left( s \right)\)
- Quãng đường: \(S = \int\limits_0^7 {v\left( t \right)dt} \).
Lời giải chi tiết:
Giả sử phương trình đường parabol (P) là \(y = a{x^2} + bx + c,\left( {a \ne 0} \right)\)
(P) có đỉnh là \(I\left( {2;7} \right)\), đồng thời đi qua điểm (3;6) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\4a + 2b + c = 7\\9a + 3b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + b = 0\\4a + 2b + c = 7\\9a + 3b + c = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 4\\c = 3\end{array} \right. \Rightarrow \left( P \right):y = - {x^2} + 4x + 3\)
Ta có hàm số sau: \(v\left( t \right) = \left\{ \begin{array}{l} - {t^2} + 4t + 3,\,\,\,\,\,0 \le t \le 3\\\,\,\,\,\,\,\,\,\,\,6\,\,\,\,\,\,\,\,\,\,\,,\,\,\,\,\,\,\,t > 3\,\end{array} \right.\)
Quãng đường cần tìm là :
\(\begin{array}{l}S = \int\limits_0^7 {v\left( t \right)dt} = \int\limits_0^3 {v\left( t \right)dt} + \int\limits_3^7 {v\left( t \right)dt} = \int\limits_0^3 {\left( { - {t^2} + 4t + 3} \right)dt} + \int\limits_3^7 {6dt} \\ = \left. {\left( { - \frac{1}{3}{t^3} + 2{t^2} + 3t} \right)} \right|_0^3 + 6.\left( {7 - 3} \right) = 18 + 24 = 42\,\,\left( {km} \right)\end{array}\)
Chọn: B