Câu hỏi
Cho hai số phức \({z_1},{z_2}\) thỏa mãn \(\left| {{z_1} - {z_2}} \right| = \left| {{z_1}} \right| = \left| {{z_2}} \right| = 2\). Tính \(\left| {{z_1} + {z_2}} \right|\)?
- A \(2\sqrt 3 \).
- B \(2\)
- C \(\sqrt 3 \).
- D \(3\sqrt 3 \)
Phương pháp giải:
Sử dụng phương pháp hình học.
Lời giải chi tiết:
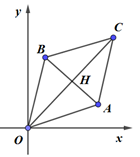
Giả sử A, B lần lượt là điểm biểu diễn của \({z_1},{z_2}\). Khi đó từ giả thiết \(\left| {{z_1} - {z_2}} \right| = \left| {{z_1}} \right| = \left| {{z_2}} \right| = 2\) ta suy ra \(OA = OB = AB = 2\)
\( \Leftrightarrow \Delta OAB\) đều, cạnh 2.
\( \Rightarrow \left| {{z_1} + {z_2}} \right| = OC = 2.OH = 2.\frac{{2\sqrt 3 }}{2} = 2\sqrt 3 \).
Chọn: A
Câu hỏi trước
