Câu hỏi
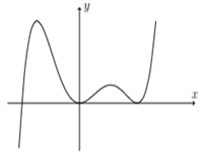
Cho hàm số \(y = f\left( x \right).\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số \(y = f\left( x \right)\) bằng
- A \(2.\)
- B \(3.\)
- C \(4.\)
- D \(1.\)
Phương pháp giải:
Tìm các điểm mà \(f'\left( x \right) = 0\) và đạo hàm đổi dấu qua điểm đó.
Lời giải chi tiết:
Từ đồ thị hàm số \(y = f'\left( x \right)\) ta thấy,
Phương trình \(f'\left( x \right) = 0\) có \(3\) nghiệm phân biệt \({x_1} < {x_2} < {x_3}\) .
Tuy nhiên đạo hàm \(f'\left( x \right)\) chỉ đổi dấu qua nghiệm \({x_1}\) nên hàm số đã cho đạt cực trị tại \(x = {x_1}\).
Vậy hàm số có \(1\) điểm cực trị.
Chọn D.