Phương pháp giải:

- Sử dụng định nghĩa giá trị lớn nhất đưa điều kiện bài toán về bất phương trình.

- Sử dụng phương pháp hàm số, xét hàm và tìm điều kiện thích hợp của \(m\).

Lời giải chi tiết:

Do \(\mathop {{\rm{max}}}\limits_{\left[ {1;3} \right]} \left| {{x^3} - 3{x^2} + m} \right| \le 4\,\) nên \(\left| {{x^3} - 3{x^2} + m} \right| \le 4,\forall x \in \left[ {1;3} \right]\)

\( \Leftrightarrow  - 4 \le {x^3} - 3{x^2} + m \le 4,\forall x \in \left[ {1;3} \right]\) \( \Leftrightarrow  - 4 - m \le {x^3} - 3{x^2} \le 4 - m,\forall x \in \left[ {1;3} \right]\).

Xét hàm \(y = {x^3} - 3{x^2}\) trên đoạn \(\left[ {1;3} \right]\) ta có: \(y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).

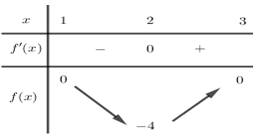
Bảng biến thiên:

Quan sát bảng biến thiên ta thấy,

\( - 4 - m \le {x^3} - 3{x^2},\forall x \in \left[ {1;3} \right] \Leftrightarrow  - 4 - m \le  - 4 \Leftrightarrow m \ge 0\)

\( \Leftrightarrow {x^3} - 3{x^2} \le 4 - m,\forall x \in \left[ {1;3} \right] \Leftrightarrow 0 \le 4 - m \Leftrightarrow m \le 4\).

Do đó \( - 4 - m \le {x^3} - 3{x^2} \le 4 - m,\,\,\forall x \in \left[ {1;3} \right] \Leftrightarrow \left\{ \begin{array}{l}m \ge 0\\m \le 4\end{array} \right. \Leftrightarrow 0 \le m \le 4\).

Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ {0;1;2;3;4} \right\}\) hay có \(5\) giá trị nguyên của \(m\) thỏa mãn bài toán.

Chọn A.