Câu hỏi
Số giao điểm của đồ thị hàm số \(y = {x^3} - 3x + 1\) và trục \(Ox\) bằng
- A \(2.\)
- B \(1.\)
- C \(4.\)
- D \(3.\)
Phương pháp giải:
Lập bảng biến thiên của hàm số \(y = f\left( x \right) = {x^3} - 3x + 1\) và sử dụng tương giao đồ thị suy ra số giao điểm.
Lời giải chi tiết:
Ta có : \(y' = 3{x^2} - 3 = 0 \Leftrightarrow x = \pm 1\).
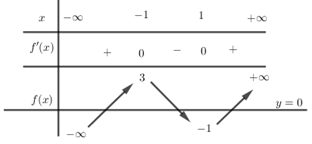
Bảng biến thiên :
Từ bảng biến thiên ta thấy, đường thẳng \(y = 0\) cắt đồ thị hàm số đã cho tại \(3\) điểm phân biệt.
Chọn D.
Câu hỏi trước
