Phương pháp giải:

+) Đặt \(t = \left| z \right|\), rút \(z\) từ đẳng thức bài cho theo \(t\) .

+) Lấy môđun hai vế đưa về phương trình ẩn \(t\).

+) Giải phương trình ẩn \(t\) và kết luận.

Lời giải chi tiết:

Đặt \(t = \left| z \right| \ge 0\) ta có : \(\left( {1 + i} \right)zt - 1 = \left( {i - 2} \right)t\)

\(\begin{array}{l} \Rightarrow \left( {1 + i} \right)zt = 1 + \left( {i - 2} \right)t \Rightarrow \left| {1 + i} \right|.\left| z \right|.t = \left| {1 - 2t + ti} \right|\\ \Rightarrow \sqrt 2 {t^2} = \sqrt {{{\left( {1 - 2t} \right)}^2} + {t^2}}  \Leftrightarrow 2{t^4} = 1 - 4t + 4{t^2} + {t^2}\\ \Leftrightarrow 2{t^4} - 5{t^2} + 4t - 1 = 0 \Leftrightarrow \left( {t - 1} \right)\left( {2{t^3} + 2{t^2} - 3t + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 1\\2{t^3} + 2{t^2} - 3t + 1 = 0\end{array} \right.\end{array}\)

Xét hàm \(f\left( t \right) = 2{t^3} + 2{t^2} - 3t + 1\) trên \(\left[ {0; + \infty } \right)\) có:

\(f'\left( t \right) = 6{t^2} + 4t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{{ - 2 + \sqrt {22} }}{6} = {t_1} > 0\\t = \dfrac{{ - 2 - \sqrt {22} }}{6} < 0\left( L \right)\end{array} \right.\)

Bảng biến thiên:

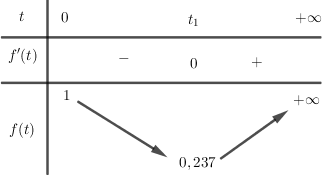
Từ bảng biến thiên ta thấy \(f\left( t \right) > 0,\forall t \ge 0\) nên phương trình \(f\left( t \right) = 0\) vô nghiệm.

Vậy \(t = 1\) hay \(\left| z \right| = 1\).

Chọn A