Câu hỏi
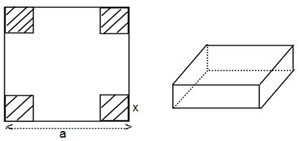
Cho một tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc bốn hình vuông bằng nhau cạnh là x cm, rồi gập tấm nhôm lại như hình vẽ dưới đây để được khối hộp chữ nhật không nắp. Tìm x sao cho thể tích của khối hộp là lớn nhất.
- A \(x = 2\)
- B \(x = 6\)
- C \(x = 4\)
- D \(x = 3\)
Phương pháp giải:
Xác định các kích thước của hình hộp có thể được tạo thành.
Lập hàm \(V(x)\) là thể tích của khối hộp.
Xác định \(x\) để \(V(x)\) lớn nhất.
Lời giải chi tiết:
Sau khi cắt 4 cạnh của hình vuông và gập lại ta được hình hộp có các kích thước là:\(12 - 2x;\,12 - 2x\,\) và \(x\) với \(0 < x < 6\).
Thể tích của hình hộp được tạo thành là: \(V\left( x \right) = x{\left( {12 - 2x} \right)^2}\).
Ta cần tìm x để hàm số V(x) đạt giá trị lớn nhất.
Ta có: \(V'\left( x \right) = {\left( {12 - 2x} \right)^2} - 4x\left( {12 - 2x} \right) \Rightarrow V'\left( x \right) = 0\)
\(\begin{array}{l} \Leftrightarrow {\left( {12 - 2x} \right)^2} - 4x\left( {12 - 2x} \right) = 0\\ \Leftrightarrow \left( {12 - 2x} \right)\left( {12 - 2x - 4x} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 6\\x = 2\end{array} \right.\end{array}\)
Ta tính giá trị của V(x) tại các giá trị \(x = 0;\,\,x = 2;\,\,x = 6\) ta được:
\(V\left( 0 \right) = 0;\,\,V\left( 2 \right) = 128;\,\,V\left( 6 \right) = 0\)
Vậy V(x) lớn nhất khi \(x = 2\).
Chọn A.







