Câu hỏi
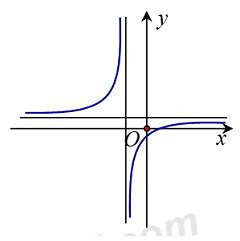
Cho hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
- A \(\left\{ {\begin{array}{*{20}{c}}{ad < 0}\\{bc > 0}\end{array}} \right.\).
- B \(\left\{ {\begin{array}{*{20}{c}}{ad < 0}\\{bc < 0}\end{array}} \right.\).
- C \(\left\{ {\begin{array}{*{20}{c}}{ad > 0}\\{bc < 0}\end{array}} \right.\).
- D \(\left\{ {\begin{array}{*{20}{c}}{ad > 0}\\{bc > 0}\end{array}} \right.\)
Phương pháp giải:
Quan sát đồ thị hàm số, tìm các đường tiệm cận, điểm đi qua suy ra dấu của \(a,b,c,d\) và kết luận.
Lời giải chi tiết:
Đồ thị hàm số có tiệm cận đứng \(x = - \dfrac{d}{c} < 0 \Rightarrow cd > 0\,\,\left( 1 \right)\).
Đồ thị hàm số có tiệm cận ngang \(y = \dfrac{a}{c} > 0 \Rightarrow ac > 0\,\,\left( 2 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(\left( {cd} \right).\left( {ac} \right) > 0 \Rightarrow ad > 0\) (loại A, B).
Dồ thị hàm số đi qua điểm \(\left( {0;\dfrac{b}{d}} \right)\) thỏa mãn \(\dfrac{b}{d} < 0 \Rightarrow bd < 0\,\,\left( 3 \right)\).
Từ \(\left( 1 \right)\) và \(\left( 3 \right)\) suy ra \(\left( {cd} \right).\left( {bd} \right) < 0 \Rightarrow bc < 0\).
Vậy \(ad > 0.bc < 0\).
Chọn C







