Câu hỏi
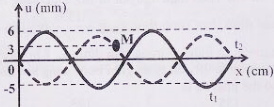
Trên sợi dây căng ngang dài 40cm, hai đầu cố định đang có sóng dừng với tần số f xác định. Hình vẽ bên mô tả hình dạng sợi dây ở thời điểm t1 và thời điểm \({t_2} = {t_1} + \frac{1}{{6f}}\). Tỉ số giữa tốc độ truyền sóng trên dây và tốc độ dao động cực đại của điểm M xấp xỉ bằng
- A 4,2
- B 6,9
- C 5,8
- D 4,8
Phương pháp giải:
Phương pháp : Sử dụng vòng tròn lượng giác trong truyền sóng cơ
Lời giải chi tiết:
Cách giải :
Theo bài ra ta có \(\left\{ \begin{array}{l}l = 4\frac{\lambda }{2} = 40cm = > \lambda = 20cm\\\Delta t = {t_2} - {t_1} = \frac{1}{{6f}} = \frac{T}{6}\end{array} \right.\)
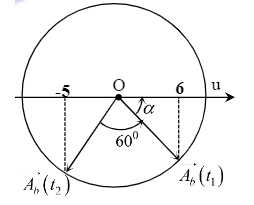
\(\left\{ \begin{array}{l}6 = {A_b}\cos \alpha \\5 = {A_b}\cos \left( {120 - \alpha } \right)\end{array} \right. = > {A_b} = 11cm\)
\(\left\{ \begin{array}{l}\frac{{{u_M}}}{{{u_B}}} = - \frac{{{A_M}}}{{{A_b}}} = > {A_M} = - {A_b}\frac{{{u_M}}}{{{u_B}}} = - 12\frac{3}{{ - 5}} = 6,6mm\\\delta = \frac{v}{{{v_{max}}}} = \frac{{\frac{\lambda }{T}}}{{{A_b}\frac{{2\pi }}{T}}} = \frac{\lambda }{{2\pi {A_b}}} = \frac{{200}}{{2\pi .7,2}} \approx 4,8\end{array} \right.\)
Chọn D







