Phương pháp giải:

Sử dụng công thức đạo hàm \({\left( {\left| {f\left( x \right)} \right|} \right)^\prime } = \frac{{f'\left( x \right).f\left( x \right)}}{{\left| {f\left( x \right)} \right|}}\)

Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(K\) khi \(f'\left( x \right) \ge 0;\,\forall x \in K\) (dấu = xảy ra tại hữu hạn điểm)

Lời giải chi tiết:

Xét hàm số \(y = \left| {{x^3} - mx + 2} \right|\) xác định trên \(\mathbb{R}.\)

Ta có \(y' = \frac{{\left( {3{x^2} - m} \right)\left( {{x^3} - mx + 2} \right)}}{{\left| {{x^3} - mx + 2} \right|}}\)

Đề hàm số đồng biến trên \(\left( {2; + \infty } \right)\) thì \(y' \ge 0;\,\forall x > 2\)

Suy ra \(\left( {3{x^2} - m} \right)\left( {{x^3} - mx + 2} \right) \ge 0;\,\forall x > 2\)

\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}3{x^2} - m \ge 0\\{x^3} - mx + 2 \ge 0\end{array} \right.\\\left\{ \begin{array}{l}3{x^2} - m \le 0\\{x^3} - mx + 2 \le 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}3{x^2} \ge m\\{x^3} + 2 \ge mx\end{array} \right.\\\left\{ \begin{array}{l}3{x^2} \le m\\{x^3} + 2 \le mx\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}3{x^2} \ge m\\{x^2} + \frac{2}{x} \ge m\end{array} \right.\,\,\left( I \right)\\\left\{ \begin{array}{l}3{x^2} \le m\\{x^2} + \frac{2}{x} \le m\end{array} \right.\,\,\left( {II} \right)\end{array} \right.\)  với mọi \(x > 2.\)

Xét hệ \(\left( I \right)\)

+ Để bất phương trình \(3{x^2} \ge m\) đúng với mọi \(x > 2\) thì hoặc \(\mathop {\min }\limits_{\left( {2; + \infty } \right)} \left( {3{x^2}} \right) = {3.2^2} = 12 \Rightarrow m \le 3{x^2};\,\forall x > 2 \Rightarrow m \le 12\)  hoặc với \(m \le 0\) thì bất phương trình \(3{x^2} \ge m\) đúng với mọi \(x \in \mathbb{R}.\) (1)

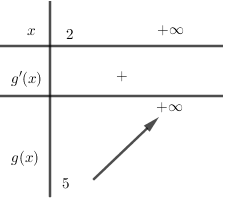
Xét hàm số \(g\left( x \right) = {x^2} + \frac{2}{x}\) trên \(\left( {2; + \infty } \right)\)

Ta có \(g'\left( x \right) = 2x - \frac{2}{{{x^2}}} = 0 \Leftrightarrow \frac{{2{x^3} - 2}}{{{x^2}}} = 0 \Leftrightarrow x = 1 \notin \left( {2; + \infty } \right)\)

BBT của \(g\left( x \right)\) trên \(\left( {2; + \infty } \right)\) : (hình bên)

Suy ra \({x^2} + \frac{2}{x} \ge m \Leftrightarrow m \le 5\)  (2)

Từ (1) và (2) suy ra \(m \le 5\) mà \(m \in \left( { - 10;10} \right);m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 9; - 8;...;4;5} \right\}\) nên có 15 giá trị thỏa mãn.

+ Xét hệ \(\left( {II} \right):\left\{ \begin{array}{l}3{x^2} \le m\\{x^2} + \frac{2}{x} \le m\end{array} \right.\,\, \Leftrightarrow \left\{ \begin{array}{l}m \ge \mathop {\max }\limits_{\left( {2; + \infty } \right)} \left( {3{x^2}} \right)\\m \ge \mathop {\max }\limits_{\left( {2; + \infty } \right)} g\left( x \right)\end{array} \right.\)

Nhận thấy hệ (II) vô nghiệm vì không tồn tại GTLN của các hàm số \(3{x^2};g\left( x \right) = {x^2} + \frac{2}{x}\) trên \(\left( {2; + \infty } \right)\).

Chọn B.