Phương pháp giải:

+) Sử dụng phương pháp bấm máy để tìm điểm cực đại của hàm số.

Lời giải chi tiết:

Ta sử dụng máy tính để thử đáp án. Hàm số đạt cực đại tại \(x = {x_0}\) thì \(f'\left( {{x_0}} \right) = 0\) và \(f\left( {{x_0}} \right) > f\left( x \right)\,\,\forall x \ne {x_0}\).

Ta dùng phím \({\left. {\dfrac{d}{{dx}}\left( {f\left( x \right)} \right)} \right|_{x = ....}}\)để thử:

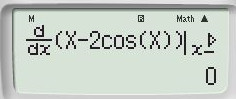
+) Đáp án A: ta thử với \(x =  - \dfrac{\pi }{6}\) được: \(f'\left( x \right) = 0 \Rightarrow \) A có thể đúng.

+) Đáp án B: ta thử với \(x = \dfrac{\pi }{6}\) được: \(f'\left( x \right) = 2 \ne 0 \Rightarrow \)loại B.

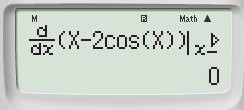
+) Đáp án C: ta thử với \(x = \dfrac{{7\pi }}{6}\) được: \(f'\left( x \right) = 0 \Rightarrow \) C có thể đúng.

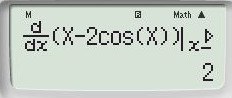
+) Đáp án D: ta thử với \(x = \dfrac{{5\pi }}{6}\) được: \(f'\left( x \right) = 2 \ne 0 \Rightarrow \)loại D.

Còn đáp án A và C ta thử ngược lại nếu \(f\left( { - \dfrac{\pi }{6}} \right) > f\left( {\dfrac{{7\pi }}{6}} \right)\) thì hàm số đạt cực đại tại \(x =  - \dfrac{\pi }{6}\) và ngược lại.

Ta nhập hàm \(f\left( x \right) = x - 2\cos x\) vào máy tính CASIO và thử với \(x =  - \dfrac{\pi }{6}\) và \(x = \dfrac{{7\pi }}{6}\).

Với  \(x =  - \dfrac{\pi }{6}\) ta được \(f\left( { - \dfrac{\pi }{6}} \right) \approx  - 2,25564\)

Với \(x = \dfrac{{7\pi }}{6}\) ta được \(f\left( {\dfrac{{7\pi }}{6}} \right) \approx 5,3972\)

Vậy hàm số đạt cực đại tại \(x = \frac{{7\pi }}{6}\).

Chọn C.