Phương pháp giải:

- Tìm tập hợp điểm biểu diễn số phức \(z\).

- Sử dụng điều kiện hình học để tìm số phức \(z\) có mô đun lớn nhất.

Lời giải chi tiết:

Gọi \(z = x + yi\). Ta có \(\left| {z + 4 - 3i} \right| = 5 \Leftrightarrow \left| {\left( {x + 4} \right) + \left( {y - 3} \right)i} \right| = 5\)\( \Leftrightarrow {\left( {x + 4} \right)^2} + {\left( {y - 3} \right)^3} = 25\).

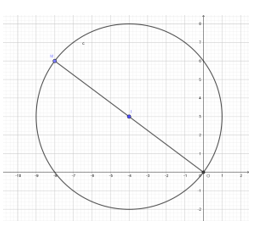
Vậy biểu diễn của số phức \(z\) là đường tròn tâm \(I\left( { - 4;\,3} \right)\), bán kính \(R = 5\).

\(M\) là điểm biểu diễn của số phức \(z\) có mô đun lớn nhất. Khi đó \(M\) là giao điểm của đường tròn \(\left( C \right)\) và đường thẳng \(OI:y =  - x\). Suy ra \(M\left( { - 8;\,6} \right)\).

Chọn D.