Câu hỏi
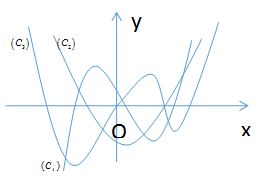
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm cấp hai trên \(\mathbb{R}\). Đồ thị của các hàm số \(y = f\left( x \right)\), \(y = f'\left( x \right)\), \(y = f''\left( x \right)\) lần lượt là các đường cong nào trong hình vẽ bên?
- A \(\left( {{C_3}} \right),\,\,\left( {{C_1}} \right),\,\,\left( {{C_2}} \right)\)
- B \(\left( {{C_1}} \right),\,\,\left( {{C_2}} \right),\,\,\left( {{C_3}} \right)\)
- C \(\left( {{C_3}} \right),\,\,\left( {{C_2}} \right),\,\,\left( {{C_1}} \right)\)
- D \(\left( {{C_1}} \right),\,\,\left( {{C_3}} \right),\,\,\left( {{C_2}} \right)\)
Phương pháp giải:
Sau mỗi lần đạo hàm hàm đa thức thì bậc của hàm số giảm đi 1 đơn vị.
Lời giải chi tiết:
Từ đồ thị ta thấy (C3) là đồ thị của hàm bậc bốn; (C1) là đồ thị của hàm bậc ba; \(\left( {{C_2}} \right)\) là đồ thị hàm bậc hai (parabol) nên (C3) là đồ thị của \(f(x);\) \(\left( {{C_1}} \right)\)là đồ thị của\(f'\left( x \right)\); \(\left( {{C_2}} \right)\) là đồ thị của \(f''\left( x \right)\).
Chọn A.
Câu hỏi trước
