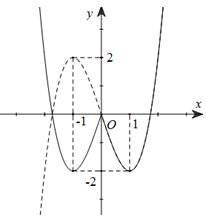
Câu hỏi
Cho đường cong \(\left( \Gamma \right)\) được vẽ bởi nét liền trong hình vẽ. Hỏi \(\left( \Gamma \right)\) là dạng đồ thị của hàm số nào?
- A \(y = - {\left| x \right|^3} + 3\left| x \right|\)
- B \(y = \left| {{x^3} - 3x} \right|\)
- C \(y = {x^3} - 3x\)
- D \(y = \left| {{x^3}} \right| - 3\left| x \right|\)
Phương pháp giải:
Cách dựng các đồ thị hàm số \(y = |f(x)|\) và \(y = f(|x|)\) từ đồ thị hàm số \(y = f(x):\)
+ Dựng đồ thị hàm số \(y = |f(x)|:\) Giữ nguyên phần đồ thị \(y = f(x)\) trên trục hoành, phần đồ thị hàm số \(y = f(x)\) dưới \(Ox,\) lấy đối xứng qua \(Ox\) sau đó xóa đi phần đồ thị nằm phía dưới \(Ox.\)
+ Dựng đồ thị hàm số \(y = f(|x|):\) Bỏ phần đồ thị hàm số \(y = f(x)\) bên trái \(Oy,\) phần đồ thị hàm số bên phải \(Oy\) lấy đối xứng qua \(Oy.\)
Lời giải chi tiết:
Đường cong đã cho được tạo bởi đồ thị hàm số \(y = f(x)\) (nét đứt) qua phép đối xứng trục \(Oy\)
Ta thấy \(f(x)\) là hàm số bậc 3, có hệ số của \(x^3\) dương nên loại đáp án A
Vì đường cong được tạo bởi phép đối xứng qua trục tung nên nó là đồ thị hàm số \(y = f(|x|)\)
Chọn D.