Phương pháp giải:

Sử dụng chức năng Mode 7 để thử các đáp án.

Lời giải chi tiết:

Ta có: \(y' = 3{x^2} - 4mx - m - 1\).

Để hàm số nghịch biến trên đoạn \(\left[ {0;2} \right]\) thì \(y' \le 0\,\forall x \in \left[ {0;2} \right]\).

Ta sử dụng máy tính để thử đáp án với với các giá trị m tương ứng và với giá trị \(x = 1\).

+) Trước hết, ta thử với \(m = \dfrac{{11}}{9} \Rightarrow y' = 3{x^2} - \dfrac{{44}}{9}x - \dfrac{{20}}{9}\).

Nhập hàm số trên vào máy tính và tính giá trị của hàm số khi \(x = 1\) ta được: \(y' =  - \dfrac{{37}}{9} < 0\)

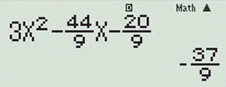
\( \Rightarrow \)hàm số nghịch biến \( \Rightarrow m = \dfrac{{11}}{9}\) thỏa mãn \( \Rightarrow \) ta loại đáp án A và B.

+) Thử với \(m = 2\)\( \Rightarrow y' = 3{x^2} - 8x - 3\).

Nhập hàm số trên vào máy tính và tính giá trị của hàm số khi \(x = 1\) ta được: \(y' =  - 8 < 0\)

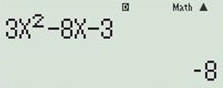
\( \Rightarrow \)hàm số nghịch biến \( \Rightarrow \) C đúng, D sai.

Chọn C.