Câu hỏi
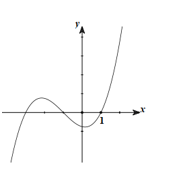
Cho hàm số \(y = f\left( x \right)\) liên tục và có đạo hàm trên \(\mathbb{R}.\) Biết hàm số \(f'\left( x \right)\) có đồ thị được cho trong hình vẽ. Tìm điều kiện của \(m\) để hàm số \(g\left( x \right) = f\left( {{{2019}^x}} \right) - mx + 2\) đồng biến trên \(\left[ {0;1} \right]\).
- A \(m \le 0\)
- B \(m \le \ln 2019\)
- C \(0 < m < \ln 2019\)
- D \(m > \ln 2019\)
Phương pháp giải:
Sử dụng công thức đạo hàm \({\left( {f\left( u \right)} \right)^\prime } = u'f'\left( u \right)\)
Hàm số \(y = f\left( x \right)\) xác định trên \(K\) thì hàm số đồng biến trên \(K\) khi \(f'\left( x \right) \ge 0;\forall x \in K\) (dấu = xảy ra
tại hữu hạn điểm)
Dựa vào đồ thị để đánh giá khoảng đồng biến của hàm \(f'\left( x \right)\) từ đó suy ra hàm \(g'\left( x \right).\)
Lời giải chi tiết:
Ta có \(g'\left( x \right) = {2019^x}.\ln 2019.f'\left( {{{2019}^x}} \right) - m\)
Để hàm số \(g\left( x \right)\) đồng biến trên \(\left[ {0;1} \right]\) thì \(g'\left( x \right) \ge 0;\forall x \in \left[ {0;1} \right] \Leftrightarrow {2019^x}.\ln 2019.f'\left( {{{2019}^x}} \right) - m \ge 0\)
\( \Leftrightarrow m \le {2019^x}.\ln 2019.f'\left( {{{2019}^x}} \right)\) với mọi \(x \in \left[ {0;1} \right]\)
Đặt \(h\left( x \right) = {2019^x}.\ln 2019.f'\left( {{{2019}^x}} \right)\) thì \(m \le \mathop {\min }\limits_{\left[ {0;1} \right]} h\left( x \right)\)
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\) ta xét trên đoạn \(\left[ {0;1} \right]\) thì \({2019^x} \in \left[ {1;2019} \right] \Rightarrow f'\left( {{{2019}^x}} \right) \ge 0\) và \(f'\left( {{{2019}^x}} \right)\) đồng biến .
Lại có \({2019^x}\) đồng biến và dương trên \(\left[ {0;1} \right]\)
Nên \(h\left( x \right) = {2019^x}\ln 2019.f'\left( {{{2019}^x}} \right)\) đồng biến trên \(\left[ {0;1} \right]\)
Suy ra \(\mathop {\min }\limits_{\left[ {0;1} \right]} h\left( x \right) = h\left( 0 \right) = {2019^0}.\ln 2019.f'\left( {{{2019}^0}} \right) = \ln 2019.f'\left( 1 \right) = 0\) (vì theo hình vẽ thì \(f'\left( 1 \right) = 0\))
Vậy \(m \le 0.\)
Chọn A.