Câu hỏi
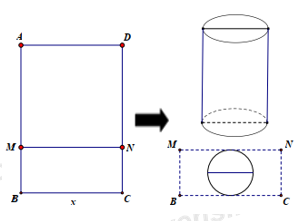
Sử dụng mảnh inox hình chữ nhật \(ABCD\) có diện tích bằng \(1{m^2}\) và cạnh \(BC = x\left( m \right)\) để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật \(ABCD\) thành hai hình chữ nhật \(ADNM\) và \(BCNM\), trong đó phần hình chữ nhật \(ADNM\) được gò thành phần xung quanh hình trụ có chiều cao bằng \(AM,\) phần hình chữ nhật \(BCNM\) được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox còn thừa được bỏ đi). Tính gần đúng giá trị \(x\) để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
- A \(1,37m\)
- B \(1,02m\)
- C \(0,97m\)
- D \(1m\)
Phương pháp giải:
Thể tích hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là \(V = \pi {r^2}h\)
Sử dụng bất đẳng thức Cô-si để tìm GTLN của thể tích.
Cho ba số \(a,b,c\) không âm, theo BĐT Cô –si ta có \(a + b + c \ge 3\sqrt[3]{{abc}} \Leftrightarrow abc \le {\left( {\dfrac{{a + b + c}}{3}} \right)^3}\)
Dấu = xáy ra khi \(a = b = c.\)
Lời giải chi tiết:
Vì \({S_{ABCD}} = AB.BC \Rightarrow AB = \dfrac{1}{x}\left( m \right)\)
Gọi \(r\) là bán kính đáy của hình trụ thì chu vi đáy của hình trụ là \(2\pi r = x \Leftrightarrow r = \dfrac{x}{{2\pi }}\left( m \right)\)
Gọi \(AM = y\left( {0 < y < \dfrac{1}{x}} \right)\) suy ra \(BM = \dfrac{1}{x} - y\)
Lại có đường kính đáy hình trụ là \(2r = BM \Leftrightarrow 2.\dfrac{x}{{2\pi }} = \dfrac{1}{x} - y \Leftrightarrow y = \dfrac{1}{x} - \dfrac{x}{\pi }\,\left( m \right)\)
(ĐK : \(\dfrac{1}{x} - \dfrac{x}{\pi } > 0 \Rightarrow 0 < x < \pi \))
Thể tích thùng nước hình trụ là \(V = \pi {r^2}h = \pi {\left( {\dfrac{x}{{2\pi }}} \right)^2}.y = \pi {\left( {\dfrac{x}{{2\pi }}} \right)^2}.\left( {\dfrac{1}{x} - \dfrac{x}{\pi }} \right)\)
\( = \pi .\dfrac{{{x^2}}}{{4{\pi ^2}}}\dfrac{{\pi - {x^2}}}{{x\pi }} = \dfrac{1}{{4{\pi ^2}}}.x\left( {\pi - {x^2}} \right) = \dfrac{1}{{2\sqrt 2 {\pi ^2}}}\sqrt {2{x^2}.\left( {\pi - {x^2}} \right)\left( {\pi - {x^2}} \right)} \)
Áp dụng bất đẳng thức Cô-si cho ba số \(2x;\left( {\pi - {x^2}} \right);\left( {\pi - {x^2}} \right)\) ta có
\(2x.\left( {\pi - {x^2}} \right).\left( {\pi - {x^2}} \right) \le {\left( {\dfrac{{2x + \left( {\pi - {x^2}} \right) + \left( {\pi - {x^2}} \right)}}{3}} \right)^3} = {\left( {\dfrac{{2\pi }}{3}} \right)^3} = \dfrac{{8{\pi ^3}}}{{27}}\)
Suy ra \(V \le \dfrac{1}{{2\sqrt 2 {\pi ^2}}}.\sqrt {\dfrac{{8{\pi ^3}}}{{27}}} \Leftrightarrow V \le \dfrac{1}{{3\sqrt {3\pi } }}\)
Dấu = xáy ra khi \(2{x^2} = \pi - {x^2} \Leftrightarrow 3{x^2} = \pi \Rightarrow x = \sqrt {\dfrac{\pi }{3}} \) (vì \(x > 0\))
Vậy thùng nước có thể tích lớn nhất khi \(x = \sqrt {\dfrac{\pi }{3}} \approx 1,02\left( m \right)\)
Chọn B.