Câu hỏi
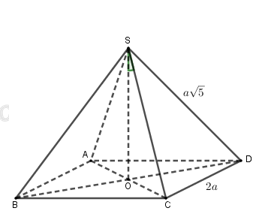
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(2a\) và cạnh bên bằng \(a\sqrt 5 \). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(A\) và vuông góc với \(SC\). Gọi \(\beta \) là góc tạo bởi mp\(\left( P \right)\) và \(\left( {ABCD} \right)\). Tính \(\tan \beta \).
- A \(\tan \beta = \dfrac{{\sqrt 6 }}{3}\)
- B \(\tan \beta = \dfrac{{\sqrt 6 }}{2}\)
- C \(\tan \beta = \dfrac{{\sqrt 2 }}{3}\)
- D \(\tan \beta = \dfrac{{\sqrt 3 }}{2}\)
Phương pháp giải:
Sử dụng lý thuyết: Góc giữa hai mặt phẳng bằng góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng ấy.
Lời giải chi tiết:
Gọi \(O\) là tâm hình vuông \(ABCD\).
Ta có: \(\left\{ \begin{array}{l}SO \bot \left( {ABCD} \right)\\SC \bot \left( P \right)\end{array} \right.\) \( \Rightarrow \) góc giữa \(\left( {ABCD} \right)\) và \(\left( P \right)\) là góc giữa \(SC\) và \(SO\) hay \(\widehat {CSO}\).
Hình vuông \(ABCD\) cạnh \(2a\) nên \(OC = \dfrac{1}{2}AC = \dfrac{1}{2}.2a\sqrt 2 = a\sqrt 2 \).
Tam giác \(SOC\) vuông tại \(O\) nên \(SO = \sqrt {S{C^2} - O{C^2}} = \sqrt {5{a^2} - 2{a^2}} = a\sqrt 3 \).
\( \Rightarrow \tan \beta = \tan \widehat {CSO} = \dfrac{{OC}}{{SO}} = \dfrac{{a\sqrt 2 }}{{a\sqrt 3 }} = \dfrac{{\sqrt 6 }}{3}\).
Chọn A.