Phương pháp giải:

+) Lấy \(B' \in SB,\,\,C' \in SC\) sao cho \(SA = SB' = SC' = 2a\). Chóp có các cạnh bên bằng nhau có chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.

+) Tính thể tích \({V_{S.AB'C'}}\).

+) \(\dfrac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}} = \dfrac{2}{3}.\dfrac{2}{4} = \dfrac{1}{3}\). Tính thể tích \({V_{S.ABC}}\).

Lời giải chi tiết:

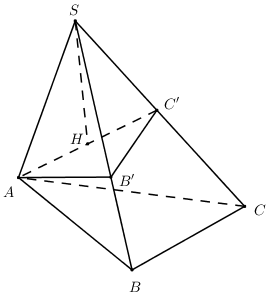
Lấy \(B' \in SB,\,\,C' \in SC\) sao cho \(SA = SB' = SC' = 2a\).

\( \Rightarrow \Delta SAB',\,\,\Delta SB'C'\) là các tam giác đều cạnh \(2a\).

\( \Rightarrow AB' = B'C' = 2a\).

Xét tam giác vuông \(SAC'\) có: \(AC' = \sqrt {S{A^2} + SC{'^2}}  = 2a\sqrt 2 \).

Xét tam giác \(AB'C'\) có \(AB{'^2} + B'C{'^2} = AC{'^2} = 8{a^2}\)

Do đó tam giác \(AB'C'\) vuông tại \(B'\) (Định lí Pytago đảo).

Gọi \(H\) là trung điểm của \(AC' \Rightarrow H\) là tâm đường tròn ngoại tiếp \(\Delta AB'C' \Rightarrow SH \bot \left( {AB'C'} \right)\).

Ta có \(AH = \dfrac{1}{2}AC' = a\sqrt 2  \Rightarrow SH = \sqrt {S{A^2} - A{H^2}}  = a\sqrt 2 \).

\({S_{AB'C'}} = \dfrac{1}{2}AB'.B'C' = 2{a^2}\).

\( \Rightarrow {V_{S.AB'C'}} = \dfrac{1}{3}SH.{S_{AB'C'}} = \dfrac{1}{3}.a\sqrt 2 .2{a^2} = \dfrac{{2{a^3}\sqrt 2 }}{3}\)

\( \Rightarrow {V_{S.ABC}} = 3{V_{S.AB'C'}} = 3.\dfrac{{2{a^3}\sqrt 2 }}{3} = 2{a^3}\sqrt 2 \).

Chọn C