Câu hỏi
Cho khối lăng trụ \(ABC.A'B'C'\) có thể tích bằng \(72c{m^3}\). Gọi \(M\) là trung điểm của đoạn thẳng \(BB'\). Tính thể tích khối tứ diện \(ABCM\).
- A \(12c{m^3}\)
- B \(36c{m^3}\)
- C \(18c{m^3}\)
- D \(24c{m^3}\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp \(V = \dfrac{1}{3}{S_{day}}.h\).
Lời giải chi tiết:
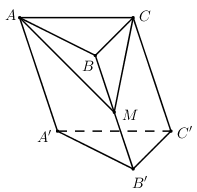
Ta có:
\(\begin{array}{l}{V_{ABCM}} = \dfrac{1}{3}d\left( {M;\left( {ABC} \right)} \right).{S_{ABC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}.\dfrac{1}{2}d\left( {B';\left( {ABC} \right)} \right).{S_{ABC}}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{6}{V_{ABC.A'B'C'}} = \dfrac{1}{6}.72 = 12\,\,\left( {c{m^3}} \right)\end{array}\)
Chọn A
Câu hỏi trước
