Câu hỏi
Tại một điểm O trên mặt nước có một nguồn sóng dao động điều hòa theo phương thẳng đứng tạo ra một hệ sóng tròn đồng tâm lan truyền ra xung quanh với bước sóng 4 (cm). Gọi M và N là hai phần tử trên mặt nước cách O lần lượt là 10 cm và 16 cm. Biết trên đoạn MN có 5 điểm dao động cùng pha với O. Coi rằng biên độ sóng rất nhỏ so với bước sóng. Khoảng cách MN gần nhất với giá trị nào sau đây?
- A 26cm
- B 25cm
- C 24cm
- D 27cm
Phương pháp giải:
Điểm cách nguồn sóng đoạn d có độ lệch pha so với nguồn là \(\Delta \varphi =\frac{2\pi d}{\lambda }\)
Lời giải chi tiết:
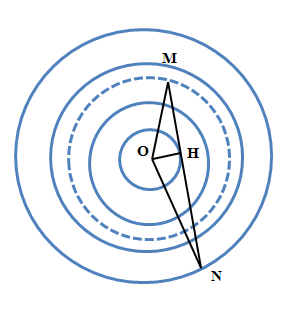
Biểu diễn các vòng tròn là các đường tròn dao động cùng pha với O bằng các đường nét liền, N nằm trên đường tròn ứng với k = 4. M nằm trên đường dao động ngược pha với nguồn ứng với k = 2,5
Để trên đoạn MN có 5 điểm cùng pha với O mà MN nhỏ nhất thì MN phải tiếp tuyến với đường trong ứng với k = 1 như hình vẽ.
OH = λ = 4cm
Ta có: \(MH=\sqrt{O{{M}^{2}}-O{{H}^{2}}}=\sqrt{{{10}^{2}}-{{4}^{2}}}= \sqrt{84}cm\)
\(NH=\sqrt{O{{N}^{2}}-O{{H}^{2}}}=\sqrt{{{16}^{2}}-{{4}^{2}}}= \sqrt{240}cm\)
Vậy MN = MH + NH = 24,65cm
Chọn B