Phương pháp giải:

+ Xác định chiều cao của hình chóp

+ Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp:

Bước 1: Xác định tâm đường tròn ngoại tiếp hình vuông \(ABCD\)

Bước 2: Xác định trục đường tròn ngoại tiếp đa giác đáy. Kẻ đường trung trực một cạnh bên giao với trục đường tròn ở đâu đó chính là tâm mặt cầu ngoại tiếp hình chóp.

+ Tính bán kính mặt cầu ngoại tiếp hình chóp dựa vào định lý Pytago.

+ Mặt cầu có bán kính \(R\) thì có diện tích là \(S = 4\pi {R^2}.\)

Lời giải chi tiết:

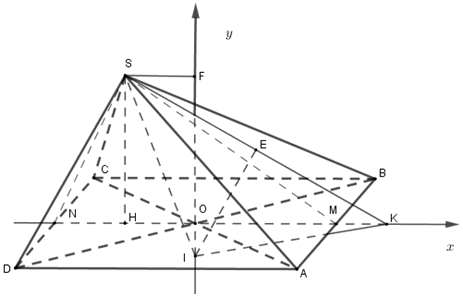
Gọi \(O\) là tâm hình vuông \(ABCD,\) gọi \(M,N\) lần lượt là trung điểm của \(AB;CD\).

Kẻ \(SH \bot MN\) tại \(H.\)

Ta có \(SN \bot DC;\,\,\,MN \bot DC \Rightarrow DC \bot \left( {SMN} \right) \Rightarrow DC \bot SH\)

Mà \(SH \bot MN \Rightarrow SH \bot \left( {ABCD} \right)\).

Vì \(ABCD\) là hình vuông cạnh \(a\) nên \(OB = OC = OA = OD = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\) ; \(OM = ON = \frac{{MN}}{2} = \frac{a}{2}\)

Vì tam giác \(SDC\) vuông cân tại \(S\) có cạnh huyền \(CD = a \Rightarrow SN = \frac{a}{2}\)

Vì tam giác \(ABS\)  đều cạnh \(a \Rightarrow SM = \frac{{a\sqrt 3 }}{2}\)

Xét tam giác \(SNM\) có \(M{N^2} = S{N^2} + S{M^2}\,\left( {{a^2} = {{\left( {\frac{a}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} = \frac{{4{a^2}}}{4} = {a^2}} \right)\)  nên \(\Delta SMN\) vuông tại \(S.\)

Suy ra \(SH.MN = SN.SM \Rightarrow SH = \frac{{\frac{a}{2}.\frac{{a\sqrt 3 }}{2}}}{a} = \frac{{a\sqrt 3 }}{4}\)  và \(S{N^2} = NH.NM \Rightarrow HN = \frac{{S{N^2}}}{{MN}} = \frac{a}{4} \Rightarrow HO = \frac{a}{4}\)

Nhận thấy \(O\) là tâm đường tròn ngoại tiếp hình vuông \(ABCD\). Kẻ tia \(Oy//SH\) , khi đó tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\) nằm trên đường thẳng \(Oy.\)

Trên tia \(OM\) ta lấy \(K\) sao cho \(OK = OA = \frac{{a\sqrt 2 }}{2}\) , khi đó \(K \in \left( {O;OA} \right)\)

Trong mặt phẳng \(\left( {SMN} \right)\), lấy \(E\) là trung điểm \(SK,\)   kẻ \(EI\) là đường trung trực của \(SK\) \(\left( {I \in Oy} \right)\)  khi đó \(IK = IS = IA = IB = IC = ID\)  nên \(I\) là tâm mặt cầu ngoại tiếp hình chóp \(S.ABCD\) và bán kính là \(R = IK\)

Kẻ \(SF \bot Oy \Rightarrow SF = OH = \frac{a}{4};OF = SH = \frac{{a\sqrt 3 }}{4}\) 

Gắn hệ trục \(Oxy\) với \(OM \equiv Ox;Oy//SH\)

Đặt \(I\left( {0;{y_0}} \right) \Rightarrow IF = \frac{{a\sqrt 3 }}{4} - {y_0}\)

Xét tam giác vuông \(\Delta ISF\) có \(I{S^2} = I{F^2} + S{F^2} = {\left( {\frac{{a\sqrt 3 }}{4} - {y_0}} \right)^2} + {\left( {\frac{a}{4}} \right)^2}\)

Xét tam giác vuông \(OIK\) có \(I{K^2} = O{I^2} + O{K^2} = {y_0}^2 + {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2}\)

Vì \(IK = IS \Leftrightarrow I{K^2} = I{S^2} \Leftrightarrow {\left( {\frac{{a\sqrt 3 }}{4} - {y_0}} \right)^2} + {\left( {\frac{a}{4}} \right)^2} = {y_0}^2 + {\left( {\frac{{a\sqrt 2 }}{2}} \right)^2}\) \( \Leftrightarrow  - \frac{{\sqrt 3 }}{2}{y_0} = \frac{{{a^2}}}{4} \Rightarrow {y_0} =  - \frac{{a\sqrt 3 }}{6}\)

Suy ra bán kính mặt cầu \(R = IK = \sqrt {y_0^2 + {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}}  = \sqrt {\frac{{{a^2}}}{{12}} + \frac{{{a^2}}}{2}}  = \frac{{a\sqrt {21} }}{6}\)

Diện tích mặt cầu ngoại tiếp hình chóp là \(S = 4\pi {R^2} = 4\pi .\frac{{{a^2}.21}}{{36}} = \frac{{7\pi {a^2}}}{3}.\)

Chọn A.