Định lí Viète - Từ điển môn Toán 9 1. Khái niệm hàm số y = ax²
Hàm số y = ax2, là một dạng của hàm số bậc hai, là hàm số có dạng như sau: \(y = a{x^2}\left( {a \ne 0} \right)\)
Hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) xác định với mọi giá trị x thuộc \(\mathbb{R}\).
Ví dụ: Hàm số \(y = 2{x^2},y = - \frac{3}{2}{x^2}\) là các hàm số có dạng \(y = a{x^2}\left( {a \ne 0} \right)\).
2. Khái niệm đồ thị của hàm số y = ax² (a ≠ 0)
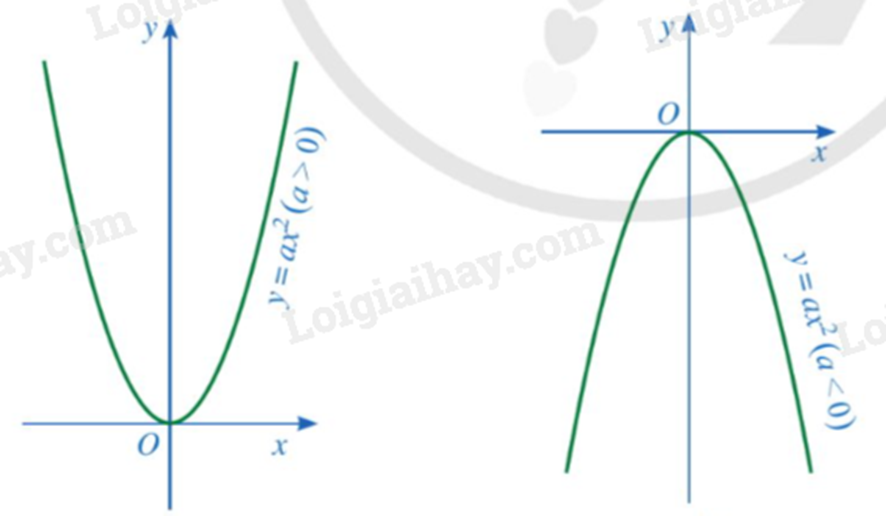
Đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) là một đường cong được gọi là parabol. Parabol đó luôn đi qua gốc toạ độ và có dạng như sau:
3. Định lí Viète
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) thì
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{b}{a}\\{x_1}{x_2} = \frac{c}{a}.\end{array} \right.\)
Ví dụ: Phương trình \(2{x^2} + 11x + 7 = 0\) có: \(\Delta = {11^2} - 4.2.7 = 65 > 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
Theo định lí Viète, ta có: \({x_1} + {x_2} = - \frac{{11}}{2};{x_1}{x_2} = \frac{7}{2}\).
4. Cách xác định sự tương giao của hai đồ thị chứa tham số liên quan đến định lí Viète
Khi cần biện luận số giao điểm của một đường thẳng (d) và Parabol (P): \(y = a{x^2}\), ta cần chú ý:
- Nếu đường thẳng (d) là \(y = m\) (song song với trục Ox) ta có thể dựa vào đồ thị để biện luận hoặc biện luận dựa vào \(a{x^2} = m\).
- Nếu đường thẳng \(\left( d \right):y = mx + n\), ta thường xét phương trình hoành độ giao điểm của (P) và (d)
là: \(a{x^2} = mx + n\) hay \(a{x^2} - mx - n = 0\) từ đó ta xét số giao điểm dựa trên số nghiệm của phương trình \(a{x^2} - mx - n = 0\) bằng cách xét dấu của \(\Delta \).
- Trong trường hợp đường thẳng (d) cắt đồ thị hàm số (P) tại hai điểm phân biệt A, B thì \(A\left( {{x_1};m{x_1} + n} \right)\), \(B\left( {{x_2};m{x_2} + n} \right)\) khi đó ta có:
\(AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {m^2}{{\left( {{x_2} - {x_1}} \right)}^2}} = \sqrt {\left( {{m^2} + 1} \right)\left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 4{x_1}{x_2}} \right]} \)
Mọi câu hỏi liên quan đến nghiệm \({x_1},{x_2}\), ta đều quy về định lý Viète.
Chú ý: Đường thẳng (d) có hệ số góc a đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) thì có dạng: \(y = a\left( {x - {x_0}} \right) + {y_0}\).
