Cách giải các bài toán liên quan đến hình học bằng cách lập phương trình - Toán 9

Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng

\(a{x^2} + bx + c = 0\),

trong đó x là ẩn; a, b, c là những số cho trước gọi là hệ số và \(a \ne 0\).

Bước 1: Lập phương trình:

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

- Lập phương trình biểu diễn mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình.

Bước 3. Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Kiến thức cần nhớ:

+ Diện tích tam giác: \(S = \frac{1}{2}ah\) (\(a\) là cạnh đáy, \(h\) là đường cao)

+ Diện tích tam giác vuông:  \(S = \frac{1}{2}xy\) (\(x,y\) là hai cạnh góc vuông). Độ dài cạnh huyền: \({z^2} = {x^2} + {y^2}\) (z là cạnh huyền) theo Định lí Pythagore.

+ Diện tích hình chữ nhật: \(S = xy\) (\(x\) là chiều rộng, \(y\) là chiều dài)

+ Diện tích hình vuông: \(S = {x^2}\) (\(x\) là cạnh hình vuông)

+ Diện tích hình thang: \(S = \frac{1}{2}h\left( {x + y} \right)\) (\(x\) là đáy bé, \(y\) là đáy lớn, \(h\) là chiều cao của hình thang)

Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\).

Bước 1: Xác định các hệ số a, b, c và tính biệt thức \(\Delta  = {b^2} - 4ac\).

Bước 2: Kết luận

- Nếu \(\Delta  > 0\) thì phương trình có hai nghiệm phân biệt:

\({x_1} = \frac{{ - b + \sqrt \Delta  }}{{2a}};{x_2} = \frac{{ - b - \sqrt \Delta  }}{{2a}}\).

- Nếu \(\Delta  = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} =  - \frac{b}{{2a}}\).

- Nếu \(\Delta  < 0\) thì phương trình vô nghiệm.

Xét phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\)

Bước 1: Xác định các hệ số a, b’, c với \(b = 2b'\) và tính biệt thức \(\Delta ' = b{'^2} - ac\).

Bước 2: Kết luận

- Nếu \(\Delta ' > 0\) thì phương trình có hai nghiệm phân biệt:

\({x_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a};{x_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a}\).

- Nếu \(\Delta ' = 0\) thì phương trình có nghiệm kép \({x_1} = {x_2} =  - \frac{{b'}}{a}\).

- Nếu \(\Delta ' < 0\) thì phương trình vô nghiệm.

Ví dụ: Giải phương trình \({x^2} - 7x - 8 = 0\).

Ta có: \(a = 1,b =  - 7,c =  - 8\).

\(\Delta  = {b^2} - 4ac = {\left( { - 7} \right)^2} - 4.1.\left( { - 8} \right) = 81 > 0\).

Vậy phương trình có hai nghiệm phân biệt là

\({x_1} = \frac{{ - \left( { - 7} \right) + \sqrt {81} }}{{2.1}} = 8;{x_2} = \frac{{ - \left( { - 7} \right) - \sqrt {81} }}{{2.1}} =  - 1\).

Sử dụng máy tính cầm tay, ta có thể dễ dạng tìm nghiệm của các phương trình bậc hai.

Bước 1. Ta sử dụng loại máy tính cầm tay (MTCT) có chức năng này (có phím MODE/MENU).

Đối với máy Fx-570VN PLUS, ta bấm phím MODE rồi bấm phím 5 rồi bấm phím 3 để chuyển về chế độ giải phương trình bậc hai.

Đối với máy Fx-580VNX, ta bấm MENU rồi bấm phím 9 để chọn tính năng Equation/Func (Ptrình/HệPtrình).

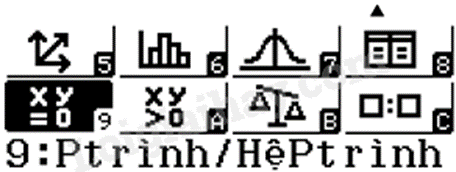
Bấm phím 2 để chọn Polynomial Degree

Cuối cùng, bấm phím 2 để giải phương trình bậc hai

Bước 2. Ta nhập các hệ số \(a,b,c\) bằng cách bấm

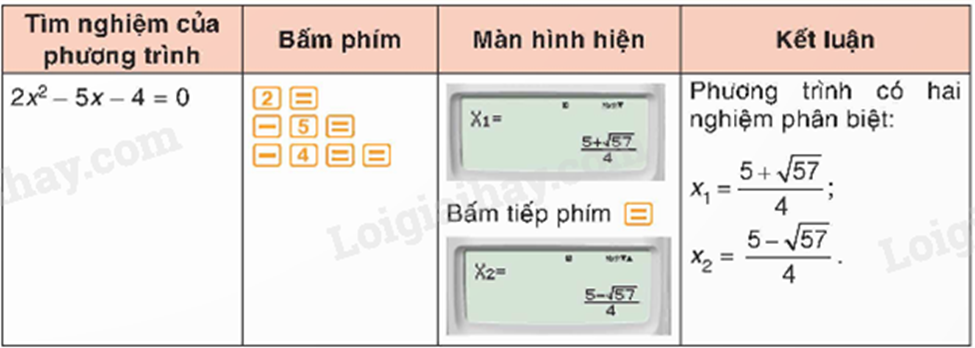
Đối với phương trình bậc hai có nghiệm kép, ta nhận được kết quả hiển thị trên màn hình như sau:

Đối với phương trình bậc hai vô nghiệm, ta nhận được kết quả hiển thị trên màn hình như sau: