Cách tính tỉ số lượng giác. Cách tính giá trị biểu thức lượng giác - Toán 9

Tỉ số lượng giác của góc nhọn là các tỉ số của góc nhọn và các cạnh tương ứng xuất hiện trong các tam giác vuông.

+) Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sin α.

+) Tỉ số giữa cạnh kề và cạnh huyền được gọi là cos (cosin) của góc α, kí hiệu là cos α.

+) Tỉ số giữa cạnh đối và cạnh kề được gọi là tan (tang) của góc α, kí hiệu là tan α.

+) Tỉ số giữa cạnh kề và cạnh đối được gọi là cot (côtang) của góc α, kí hiệu là cot α.

\(\sin \alpha = \frac{\text{cạnh đối}}{\text{cạnh huyền}}\);\(\cos \alpha = \frac{\text{cạnh kề}}{\text{cạnh huyền}}\);

\(\tan \alpha = \frac{\text{cạnh đối}}{\text{cạnh kề}}\);\(\cot \alpha = \frac{\text{cạnh kề}}{\text{cạnh đối}}\).

Quy ước:

\(\begin{array}{l}{\sin ^2}\alpha  = {\left( {\sin \alpha } \right)^2};\\{\cos ^2}\alpha  = {\left( {\cos \alpha } \right)^2};\\{\tan ^2}\alpha  = {\left( {\tan \alpha } \right)^2};\\{\cot ^2}\alpha  = {\left( {\cot \alpha } \right)^2}.\end{array}\)

Tip học thuộc nhanh:

Sin đi học

Cos không hư

Tang đoàn kết

Cotang kết đoàn

Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Với \(0^\circ  < \alpha  < 90^\circ \), ta có:

\(\sin \left( {90^\circ  - \alpha } \right) = \cos \alpha \); \(\cos \left( {90^\circ  - \alpha } \right) = \sin \alpha \);

\(\tan \left( {90^\circ  - \alpha } \right) = \cot \alpha \); \(\cot \left( {90^\circ  - \alpha } \right) = \tan \alpha \).

+) Với góc nhọn \(\alpha \), ta có:

\(0 < \sin \alpha  < 1\); \(0 < \cos \alpha  < 1\); \(\tan \alpha  > 0\); \(\cot \alpha  > 0\); \(\cot \alpha  = \frac{1}{{\tan \alpha }}\).

+) \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)         

+) \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\)

+) \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\)

+) \(\tan \alpha .\cot \alpha  = 1\)

+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha  + 1\)

+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha  + 1\)

Để tính tỉ số lượng giác, ta dựa vào khái niệm sin, cos, tan, cot và các công thức lượng giác liên quan:

+) \(\sin \alpha = \frac{\text{cạnh đối}}{\text{cạnh huyền}}\);\(\cos \alpha = \frac{\text{cạnh kề}}{\text{cạnh huyền}}\);

+) \(\tan \alpha = \frac{\text{cạnh đối}}{\text{cạnh kề}}\);\(\cot \alpha = \frac{\text{cạnh kề}}{\text{cạnh đối}}\).

+) Với góc nhọn \(\alpha \), ta có:

\(0 < \sin \alpha  < 1\); \(0 < \cos \alpha  < 1\); \(\tan \alpha  > 0\); \(\cot \alpha  > 0\); \(\cot \alpha  = \frac{1}{{\tan \alpha }}\).

+) \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)         

+) \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\)

+) \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\)

+) \(\tan \alpha .\cot \alpha  = 1\)

+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha  + 1\)

+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha  + 1\)

Sử dụng kết hợp các kiến thức về tỉ số lượng giác để tính giá trị biểu thức lượng giác:

- Giá trị lượng giác của các góc đặc biệt:

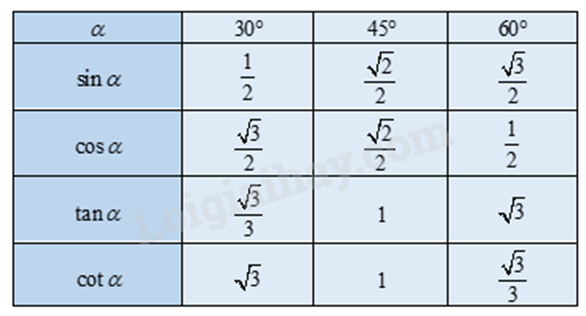
- Tỉ số lượng giác của hai góc phụ nhau:

Với \(0^\circ  < \alpha  < 90^\circ \), ta có:

\(\sin \left( {90^\circ  - \alpha } \right) = \cos \alpha \); \(\cos \left( {90^\circ  - \alpha } \right) = \sin \alpha \);

\(\tan \left( {90^\circ  - \alpha } \right) = \cot \alpha \); \(\cot \left( {90^\circ  - \alpha } \right) = \tan \alpha \).

- Các công thức lượng giác liên quan:

+) Với góc nhọn \(\alpha \), ta có:

\(0 < \sin \alpha  < 1\); \(0 < \cos \alpha  < 1\); \(\tan \alpha  > 0\); \(\cot \alpha  > 0\); \(\cot \alpha  = \frac{1}{{\tan \alpha }}\).

+) \({\sin ^2}\alpha  + {\cos ^2}\alpha  = 1\)         

+) \(\tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\)

+) \(\cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\)

+) \(\tan \alpha .\cot \alpha  = 1\)

+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha  + 1\)

+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha  + 1\)