Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) không phải là hình thang. Trên cạnh \(SC\) lấy điểm \(M\). Gọi \(N\) là giao điểm của đường thẳng \(SD\) với mặt phẳng \(\left( {AMB} \right)\). Mệnh đề nào sau đây đúng?
-
A.
Ba đường thẳng $AB,{\rm{ }}CD,{\rm{ }}MN$ đôi một song song
-
B.
Ba đường thẳng $AB,{\rm{ }}CD,{\rm{ }}MN$ đôi một cắt nhau
-
C.
Ba đường thẳng $AB,{\rm{ }}CD,{\rm{ }}MN$ đồng quy.
-
D.
Ba đường thẳng $AB,{\rm{ }}CD,{\rm{ }}MN$ cùng thuộc một mặt phẳng.
- Tìm giao điểm \(O\) của \(AB,CD\).
- Chứng minh \(MN\) là giao tuyến của hai mặt phẳng \(\left( {AMB} \right)\) và \(\left( {SCD} \right)\).
- Chứng minh \(O\) nằm trên \(MN\) bằng cách chứng minh \(O\) nằm trên hai mặt phẳng \(\left( {AMB} \right)\) và \(\left( {SCD} \right)\).
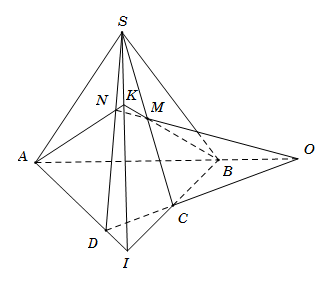
Gọi \(I = AD \cap BC.\) Trong mặt phẳng \(\left( {SBC} \right)\), gọi \(K = BM \cap SI\). Trong mặt phẳng \(\left( {SAD} \right)\), gọi \(N = AK \cap SD\).
Khi đó \(N\) là giao điểm của đường thẳng \(SD\) với mặt phẳng \(\left( {AMB} \right)\).
Gọi \(O = AB \cap CD\). Ta có:
● \(O \in AB\) mà \(AB \subset \left( {AMB} \right)\) suy ra \(O \in \left( {AMB} \right)\).
● \(O \in CD\) mà \(CD \subset \left( {SCD} \right)\) suy ra ${\rm{IJ}},MN,SE$.
Do đó \(O \in \left( {AMB} \right) \cap \left( {SCD} \right)\). \(\left( 1 \right)\)
Mà \(\left( {AMB} \right) \cap \left( {SCD} \right) = MN\). \(\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\), suy ra \(O \in MN\). Vậy ba đường thẳng $AB,{\rm{ }}CD,{\rm{ }}MN$ đồng quy.
Đáp án : C
Các bài tập cùng chuyên đề
Hai đường thẳng được gọi là chéo nhau nếu:
Hai đường thẳng được gọi là song song nếu:
Cho hai đường thẳng \(a,b\) có một điểm chung duy nhất. Có thể kết luận gì về vị trí tương đối của hai đường thẳng đó?
Hai đường thẳng song song thì
Một mặt phẳng không thể được xác định nếu ta chỉ biết:
Chọn mệnh đề đúng
Cho 3 đường thẳng \({d_1},\;{d_2},\;{d_3}\) không cùng thuộc một mặt phẳng và cắt nhau từng đôi. Khẳng định nào sau đây đúng?
Cho tứ diện $ABCD$ có $I$ và $J$ lần lượt là trọng tâm của tam giác $ABC$ và $ABD$. Đường thẳng $IJ$ song song với đường thẳng:
Tìm mệnh đề đúng trong các mệnh đề sau:
Cho tứ diện $ABCD.$ Gọi $M, N, P, Q$ lần lượt là trung điểm của các cạnh $AB, AD, CD, BC.$ Mệnh đề nào sau đây là sai ?
Cho hình bình hành $ABCD.$ Gọi $Bx, Cy, Dz$ là các đường thẳng song song với nhau lần lượt đi qua $B, C, D$ và nằm về một phía của mặt phẳng $(ABCD),$ đồng thời không nằm trong mặt phẳng $(ABCD).$ Một mặt phẳng đi qua $A$ và cắt $Bx, Cy, Dz$ lần lượt tại các điểm $B’, C’, D’ $ với $BB’ = 2, DD’ = 4.$ Khi đó $CC’$ bằng:
Trong các mệnh đề sau, mệnh đề nào đúng?
Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O.$ Lấy điểm $I$ trên đoạn $SO$ sao cho \(\dfrac{{SI}}{{SO}} = \dfrac{2}{3}\), $BI$ cắt $SD$ tại $M$ và $DI$ cắt $SB$ tại $N. $ Khi đó $MNBD$ là hình gì?
Cho tứ diện $ABCD.$ Gọi $M,N,P,Q$ lần lượt là trung điểm $AC, BC, BD, AD.$ Tìm điều kiện của tứ diện $ABCD$ để $MNPQ$ là hình thoi?
Cho tứ diện \(ABCD.\) Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AB\) và \(CD.\) Mặt phẳng \(\left( \alpha \right)\) qua \(MN\) cắt \(AD,{\rm{ }}BC\) lần lượt tại \(P\) và \(Q.\) Biết \(MP\) cắt \(NQ\) tại \(I.\) Ba điểm nào sau đây thẳng hàng?
Cho tứ diện \(SABC\). Gọi \(L,{\rm{ }}M,{\rm{ }}N\) lần lượt là các điểm trên các cạnh \(SA,{\rm{ }}SB\) và \(AC\) sao cho \(LM\) không song song với \(AB\), \(LN\) không song song với \(SC\). Mặt phẳng \(\left( {LMN} \right)\) cắt các đường thẳng \(AB,{\rm{ }}BC,{\rm{ }}SC\) lần lượt tại \(K,{\rm{ }}I,{\rm{ }}J\). Ba điểm nào sau đây thẳng hàng?
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm tam giác \(BCD,\) \(M\) là trung điểm \(CD,\) \(I\) là điểm ở trên đoạn thẳng \(AG,\) \(BI\) cắt mặt phẳng \(\left( {ACD} \right)\) tại \(J.\) Khẳng định nào sau đây sai?
Cho tứ diện \(ABCD\). Gọi \(E,{\rm{ }}F,{\rm{ }}G\) là các điểm lần lượt thuộc các cạnh \(AB,{\rm{ }}AC,{\rm{ }}BD\) sao cho $EF$ cắt \(BC\) tại \(I\), \(EG\) cắt \(AD\) tại \(H\). Ba đường thẳng nào sau đây đồng quy?
Cho tứ diện $ABCD, M$ là trung điểm của cạnh $CD, G$ là trọng tâm tứ diện. Khi đó $2$ đường thẳng $AD$ và $GM$ là hai đường thẳng:
Cho hình chóp \(S.ABCD\) đáy là hình bình hành tâm \(O\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA\), \(SC,\) \(OB\). Gọi \(Q\) là giao điểm của \(SD\) với \(mp\left( {MNP} \right)\). Tính \(\dfrac{{SQ}}{{SD}}.\)
