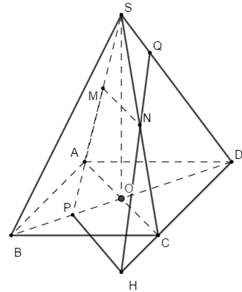
Cho hình chóp \(S.ABCD\) đáy là hình bình hành tâm \(O\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA\), \(SC,\) \(OB\). Gọi \(Q\) là giao điểm của \(SD\) với \(mp\left( {MNP} \right)\). Tính \(\dfrac{{SQ}}{{SD}}.\)
-
A.
\(\dfrac{{SQ}}{{SD}} = \dfrac{1}{4}.\)
-
B.
\(\dfrac{{SQ}}{{SD}} = \dfrac{1}{3}.\)
-
C.
\(\dfrac{{SQ}}{{SD}} = \dfrac{1}{5}.\)
-
D.
\(\dfrac{{SQ}}{{SD}} = \dfrac{6}{{25}}.\)
Bước 1: Tìm điểm Q.
Bước 2: Tính \(\dfrac{{NC}}{{NS}}\) và \(\dfrac{{HD}}{{HC}}\).
Bước 3: Sử dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(QNH\) để tính \(\dfrac{{SQ}}{{SD}}\)
Định lý: Cho tam giác ABC. Các điểm D, E, F lần lượt nằm trên các đường thẳng BC, CA, AB. Khi đó D, E, F thẳng hàng khi và chỉ khi \(\dfrac{{FA}}{{FB}}.\dfrac{{DB}}{{DC}}.\dfrac{{EC}}{{EA}} = 1\).
Bước 1:
Trong \(\left( {ABCD} \right)\) lấy \(PH\parallel AC\)\((H \in CD)\)
=> \(PH||MN\) (Do \(AC||MN\))\( \Rightarrow H \in \left( {PMN} \right)\)\( \Rightarrow NH \subset \left( {PMN} \right)\)
Trong \(\left( {SCD} \right)\) gọi \(Q = NH \cap SD\)
Mà \(NH \subset \left( {PMN} \right)\)=> \(Q \in \left( {PMN} \right)\)
Khi đó \(Q\) là giao điểm của \(SD\) với \(mp\left( {MNP} \right)\)
Bước 2:
Mà \(N\) là trung điểm của \(SC \Rightarrow \dfrac{{NC}}{{NS}} = 1\).
Mặt khác áp dụng định lí Ta-lét trong tam giác \(DPH\) ta có \(\dfrac{{HD}}{{HC}} = \dfrac{{DP}}{{OP}} = 3\) (vì \(P\) là trung điểm của \(OB\)).
Bước 3:
Áp dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(QNH\) ta có: \(\dfrac{{HD}}{{HC}}.\dfrac{{NC}}{{NS}}.\dfrac{{QS}}{{QD}} = 1\)
Do đó ta có \(\dfrac{{QS}}{{QD}} = \dfrac{1}{3} \Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{1}{4}\)
Đáp án : A








Danh sách bình luận