Cho tứ diện $ABCD$ có $I$ và $J$ lần lượt là trọng tâm của tam giác $ABC$ và $ABD$. Đường thẳng $IJ$ song song với đường thẳng:

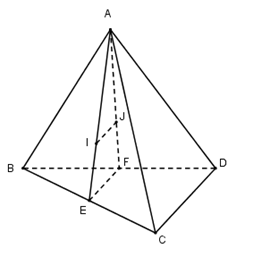
Gọi $E, F$ lần lượt là trung điểm của $BC$ và $BD$ ta có:

$\begin{array}{l}I \in AE\,;\,\dfrac{{AI}}{{AE}} = \dfrac{2}{3}\\J \in AF\,;\,\dfrac{{AJ}}{{AF}} = \dfrac{2}{3}\end{array}$

Xét trong $mp(AEF)$ ta suy ra \(IJ//EF\) (Định lí Ta – let đảo)

Mà $EF$ là đường trung bình của tam giác $ABC$ \( \Rightarrow \) $EF // CD$

Vậy $IJ // CD.$