Cho tứ diện $ABCD.$ Gọi $M,N,P,Q$ lần lượt là trung điểm $AC, BC, BD, AD.$ Tìm điều kiện của tứ diện $ABCD$ để $MNPQ$ là hình thoi?

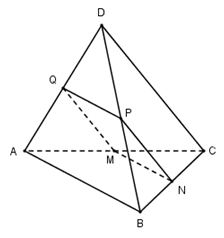
Vì $MN$ và $PQ$ lần lượt là đường trung bình của tam giác $ABC$ và $ABD$ nên:

\(\left\{ \begin{array}{l}MN//PQ//AB\\MN = PQ = \dfrac{1}{2}AB\end{array} \right. \Rightarrow \) MNPQ là hình bình hành.

Để $MNPQ $ trở thành hình thoi ta cần thêm yếu tố $MN = PN.$

Ta có: $PN$ là đường trung bình của tam giác $BCD$ nên \(PN = \dfrac{1}{2}CD\).

$MN = PN $ \( \Leftrightarrow \dfrac{1}{2}AB = \dfrac{1}{2}CD \Leftrightarrow AB = CD.\)

Vậy để $MNPQ $ là hình thoi cần thêm điều kiện $AB = CD.$