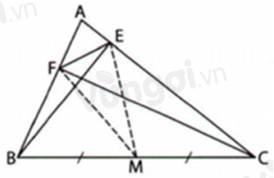
Cho tam giác \(ABC\) có hai đường vuông góc \(BE,CF.\) So sánh \(EF\) và \(BC.\)
-
A.
\(BC > EF\)
-
B.
\(BC < EF\)
-
C.
\(BC \ge EF\)
-
D.
\(BC \le EF\)
Gọi \(M\) là trung điểm của \(BC.\) Chứng minh \(ME + MF = BC\).
Áp dụng bất đẳng thức tam giác chứng minh \(ME + MF > EF\).
Từ đó suy ra điều phải chứng minh.
* Chú ý: Trong tam giác vuông, đoạn thẳng nối từ đỉnh góc vuông đến trung điểm của cạnh huyền bằng nửa cạnh huyền.
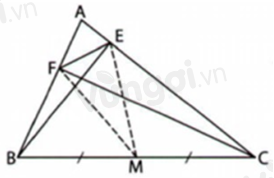
Gọi \(M\) là trung điểm của \(BC.\)
Xét \(\Delta BCE\) vuông tại \(E\), \(M\) là trung điểm của \(BC\) nên \(ME = \dfrac{1}{2}BC.\)
Xét \(\Delta BCF\) vuông tại \(F\), \(M\) là trung điểm của \(BC\) nên \(MF = \dfrac{1}{2}BC.\)
Do đó \(ME + MF = \dfrac{1}{2}BC + \dfrac{1}{2}BC \Rightarrow ME + MF = BC\) (1)
Ba điểm \(M,\,E,\,F\) nằm trên ba cạnh của tam giác \(ABC\) nên không thể thẳng hàng do đó ba điểm \(M,\,E,\,F\) tạo thành một tam giác.
Xét \(\Delta MEF\) có: \(ME + MF > EF\) (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra \(BC > EF.\)
Đáp án : A
Các bài tập cùng chuyên đề
Cho \(\Delta ABC\), em hãy chọn đáp án sai trong các đáp án sau:
Dựa vào bất đẳng thức tam giác, kiểm tra xem bộ ba nào trong các bộ ba đoạn thẳng có độ dài cho sau đây không thể là ba cạnh của một tam giác.
Cho \(\Delta ABC\) có cạnh $AB = 1cm$ và cạnh \(BC = 4cm\). Tính độ dài cạnh $AC$ biết độ dài cạnh $AC$ là một số nguyên.
Cho tam giác \(ABC\) biết \(AB = 1\,cm;\,BC = 9\,cm\) và cạnh \(AC\) là một số nguyên. Chu vi tam giác \(ABC\) là
Cho tam giác \(ABC\) có \(BC = 1\,cm\), \(AC = \,8\,cm\) và độ dài cạnh \(AB\) là một số nguyên \(\left( {cm} \right)\). Tam giác \(ABC\) là tam giác gì?
Cho \(\Delta ABC\) cân tại \(A\) có một cạnh bằng $5cm.$ Tính cạnh $BC$ của tam giác đó biết chu vi của tam giác là $17cm.$
Cho \(\Delta ABC\) có $M$ là trung điểm $BC.$ So sánh $AB + AC$ và $2AM.$
Cho \(\Delta ABC\) có điểm $O$ là một điểm bất kì nằm trong tam giác. So sánh \(OA + OC\) và \(AB + BC\).
Có bao nhiêu tam giác có độ dài hai cạnh là \(7\,cm\) và \(2\,cm\) còn độ dài cạnh thứ ba là một số nguyên (đơn vị cm)?
Cho hình vẽ dưới đây. Chọn câu đúng.
Cho tam giác \(ABC\) điểm \(M\) nằm trong tam giác. Chọn câu đúng.
Chọn câu đúng. Trong một tam giác
Cho \(\Delta ABC\), trên $BC$ lấy điểm $M$ bất kì nằm giữa $B$ và $C.$
So sánh \(AB + AC - BC\) và \(2.AM\)
Cho tam giác \(ABC\) có \(AB > AC.\) Điểm \(M\) là trung điểm của \(BC.\) Chọn câu đúng.
Cho \(\Delta ABC\) có \(M\) là trung điểm của \(BC\). Trong các khẳng định sau khẳng định nào đúng?
Độ dài hai cạnh của một tam giác là 2 (cm) và 21 (cm). Số đo nào dưới đây có thể là độ dài cạnh thứ ba của tam giác đã cho?
