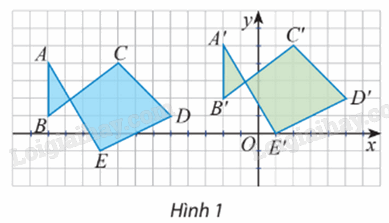
Trong Hình 1, tìm hai phép biến hình để biến tam giác ABC thành tam giác A’B’C’.

Cho điểm O cố định và một số thực k, \(k \ne 0\). Phép biến hình biến mỗi điểm M thành điểm M’ sao cho \(\overrightarrow {OM'} = k\overrightarrow {OM} \) được gọi là phép vị tự tâm O tỉ số k, kí hiệu \({V_{(O,k)}}\). O được gọi là tâm vị tự, k gọi là tỉ số vị tự.
Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến ∆ABC thành \(\Delta \)\({A_1}{B_1}{C_1}\;\) và tìm phép biến hình biến \(\Delta \)\({A_1}{B_1}{C_1}\;\) thành \(\Delta \)A’B’C’.
⦁ Để tìm phép biến hình biến \(\Delta \)ABC thành \(\Delta \)A1B1C1, ta tìm phép biến hình biến các điểm A, B, C theo thứ tự thành các điểm \({A_1},{\rm{ }}{B_1},{\rm{ }}{C_1}.\)
Ta thấy các đường thẳng \(A{A_1},{\rm{ }}B{B_1},{\rm{ }}C{C_1}\;\) đồng quy tại O.
Xét phép vị tự tâm O, tỉ số k biến các điểm A, B, C theo thứ tự thành các điểm A1, B1, C1.
Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( A \right){\rm{ }} = {\rm{ }}{A_1}.\)
Suy ra \(\overrightarrow {O{A_1}} = k\overrightarrow {OA} \) và \(O{A_1}\; = {\rm{ }}\left| k \right|.OA.\)
Vì A, A1 nằm cùng phía đối với O nên k > 0.
Do đó \(k = \frac{{O{A_1}}}{{OA}}\).
Tương tự ta cũng có \(k = \frac{{O{B_1}}}{{OB}},k = \frac{{O{C_1}}}{{OC}}\)
Do đó \(k = \frac{{O{A_1}}}{{OA}} = \frac{{O{B_1}}}{{OB}} = \frac{{O{C_1}}}{{OC}}\)
Vì vậy \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) là phép biến hình biến \(\Delta \)ABC thành \(\Delta {A_1}{B_1}{C_1}.\)
⦁ Để tìm phép biến hình biến \(\Delta {A_1}{B_1}{C_1}.\) thành \(\Delta \)A’B’C’, ta tìm phép biến hình biến các điểm A1, B1, C1 theo thứ tự thành các điểm A’, B’, C’.
Ta thấy d là đường trung trực của đoạn A1A’.
Suy ra \({D_d}({A_1}){\rm{ }} = {\rm{ }}A'.\)
Chứng minh tương tự, ta được \({D_d}({B_1}){\rm{ }} = {\rm{ }}B';{\rm{ }}{D_d}({C_1}){\rm{ }} = {\rm{ }}C'.\)
Vì vậy Đd là phép biến hình biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.
Vậy hai phép biến hình biến tam giác ABC thành tam giác A’B’C’ là \({V_{\left( {O;\frac{{O{A_1}}}{{OA}}} \right)}}\) biến \(\Delta \)ABC thành \(\Delta \)A1B1C1 và \({D_d}\) biến \(\Delta \)A1B1C1 thành \(\Delta \)A’B’C’.

Các bài tập cùng chuyên đề
Hoa và Hưng cùng chơi trò chơi sau: Hai bạn luân phiên nhau đặt các đồng xu có cùng kích thước lên trên một mặt mảnh giấy hình chữ nhật sao cho các xu nằm hoàn toàn trên mảnh giấy và xu đặt sau không chồng lên xu trước. Mỗi bạn, đến lượt mình được đặt một xu. Ai là người đầu tiên không còn chỗ để đặt xu là người thua cuộc.
Trong một lần chơi, là người đặt xu trước, Hoa đặt đồng xu đầu tiên tại vị trí O ở chính giữa mảnh giấy, và sau đó, ở mỗi lượt đặt xu, nếu Hưng đặt đồng xu ở vị trí M thì Hoa đặt ở vị trí M' đối xứng với M qua O. Hỏi trong lần chơi nói trên, ai là người thắng cuộc?
Quan sát ba tấm ảnh hoa hồng ở Hình 1.4, hãy cho biết hình nào giống ảnh của hình ở giữa qua một phép co về trục.

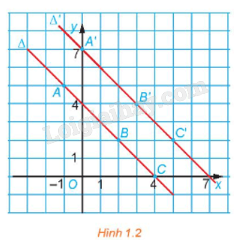
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm \(M'\left( {x{\rm{ }} + {\rm{ }}1;{\rm{ }}y{\rm{ }} + {\rm{ }}2} \right).\)
a) Xét các điểm \(A\left( {-{\rm{ }}1;{\rm{ }}5} \right),{\rm{ }}B\left( {2;{\rm{ }}2} \right),{\rm{ }}C\left( {4;{\rm{ }}0} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\). Xác định các ảnh của chúng qua f.
b) Chứng minh rằng nếu \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) là điểm thuộc đường thẳng \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) thì ảnh \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) của nó thuộc đường thẳng \(\Delta ':{\rm{ }}x + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\;\;\)
Trong mặt phẳng tọa độ Oxy cho điểm I(1; 2). Xét phép biến hình f biến điểm I thành điểm I và biến mỗi điểm M khác I thành điểm M' sao cho I là trung điểm của MM'. Tìm tọa độ ảnh của điểm A(3; – 2) qua phép biến hình f.
Trong bảng quan sát quy luật điền các cặp (A, A'), (B, B'), (C, C'), ..., từ đó điền các kí hiệu N', P', Q', R', S' vào các vị trí thích hợp.

Trong mặt phẳng cho đường thẳng d và điểm M. Dựng hình chiếu vuông góc M' của điểm M lên đường thẳng d (Hình 2).

a) Có bao nhiêu hình chiếu vuông góc của điểm M trên đường thẳng d?
b) Có điểm nào của mặt phẳng không có hình chiếu vuông góc trên đường thẳng d hay không?
Bức tranh trang trí trong hình bên trước khi tô màu thực chất được tạo ra từ một hình mũi tên duy nhất và được dời chỗ tới các vị trí khác nhau. Hãy thảo luận để tìm hiểu về các phép biến đổi hình học nào đã tạo ra tất cả các hình mũi tên như vậy từ một hình mũi tên ban đầu.

Trong mặt phẳng tọa độ Oxy, ứng mỗi điểm M(x; y) quy tắc f xác định điểm M’(–3x; 3y). Hãy cho biết f có phải là phép biến hình không. Nếu có, tìm ảnh của điểm A(–1; 2) qua f.
Trong mặt phẳng, cho đường thẳng d và điểm M. Gọi M’ là hình chiếu vuông góc của M trên đường thẳng d.
Vẽ ba điểm A, B, C tùy ý và tìm hình chiếu vuông góc A’, B’, C’ của chúng trên d.

Cho đường thẳng d đi qua tâm O của đường tròn (C) và cắt (C) tại A và B. Tìm ảnh của đường tròn (C) qua phép chiếu vuông góc lên d.
Quan sát các điểm được vẽ trên mặt phẳng tọa độ (Hình 1).
a) Có nhận xét gì về các vectơ \(\overrightarrow {AA'} ,\,\overrightarrow {BB'} ,\,...,\,\overrightarrow {EE'} \)
b) Có hay không phép biến hình biến các điểm A, B, C, D, E thành các điểm A’, B’, C’, D’, E’?
Cho đường thẳng d. Gọi f là quy tắc xác định như sau:
a) Với điểm M không thuộc d, xác định điểm M’ sao cho d là đường trung trực của MM’ (Hình 1).
b) Với điểm M thuộc d thì f biến điểm M thành chính nó.
Hỏi f có phải là phép biến hình hay không?

Trong các hình sau, hình nào có trục đối xứng?
Có phép biến hình nào biến một nửa mỗi hình phẳng sau đây thành nửa còn lại không?







