Cho \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) và \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\). Chứng minh rằng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\).
Sử dụng hằng đẳng thức bình phương của ba số để tính \({\left( {\frac{x}{a} + \frac{y}{b} + \frac{z}{c}} \right)^2} = 1\)
Cho ba số a, b, c, ta có: \({\left( {a + b + c} \right)^2} = {a^2} + {b^2} + {c^2} + 2\left( {ab + bc + ca} \right)\).
Từ \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\) chứng minh \(ayz + bxz + cxy = 0\).
Thay vào \({\left( {\frac{x}{a} + \frac{y}{b} + \frac{z}{c}} \right)^2} = 1\) để chứng minh.
Vì \(\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\) nên ta có:
\(\begin{array}{l}{\left( {\frac{x}{a} + \frac{y}{b} + \frac{z}{c}} \right)^2} = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} + 2\left( {\frac{{xy}}{{ab}} + \frac{{yz}}{{bc}} + \frac{{xz}}{{ac}}} \right) = 1\\\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} + 2\left( {\frac{{cxy + ayz + bxz}}{{abc}}} \right) = 1\end{array}\)
Mà \(\frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0\) nên ta có: \(\frac{{ayz + bxz + cxy}}{{xyz}} = 0\), suy ra \(ayz + bxz + cxy = 0\)
Do đó \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} + 2.0 = 1\)
Suy ra \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + \frac{{{z^2}}}{{{c^2}}} = 1\).
• Bài toán này sử dụng một hằng đẳng thức đại số cơ bản: bình phương của một tổng ba số.
Cụ thể, với ba số $a, b, c$ bất kỳ, ta có công thức: $ (a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + bc + ca) $1. Hằng đẳng thức này là chìa khóa để khai triển biểu thức ban đầu và dẫn đến kết quả cần chứng minh.
• Trong bài toán này, hằng đẳng thức trên được áp dụng trực tiếp cho biểu thức $ \left( \frac{x}{a} + \frac{y}{b} + \frac{z}{c} \right)^2 $.
+ Sử dụng điều kiện ban đầu: Đề bài cho $ \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 $. Ta bình phương cả hai vế của đẳng thức này: $ \left( \frac{x}{a} + \frac{y}{b} + \frac{z}{c} \right)^2 = 1^2 = 1 $.
+ Khai triển theo hằng đẳng thức: Áp dụng công thức bình phương của tổng ba số, ta khai triển vế trái của phương trình: $ \left( \frac{x}{a} + \frac{y}{b} + \frac{z}{c} \right)^2 = \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} + 2\left( \frac{xy}{ab} + \frac{yz}{bc} + \frac{xz}{ac} \right) $.
+ Quy đồng mẫu số: Phần $ 2\left( \frac{xy}{ab} + \frac{yz}{bc} + \frac{xz}{ac} \right) $ được quy đồng mẫu số chung là $abc$: $ 2\left( \frac{xy}{ab} + \frac{yz}{bc} + \frac{xz}{ac} \right) = 2\left( \frac{cxy + ayz + bxz}{abc} \right) $.
+ Sử dụng điều kiện thứ hai: Đề bài cho điều kiện thứ hai là $ \frac{a}{x} + \frac{b}{y} + \frac{c}{z} = 0 $. Từ điều kiện này, bằng cách quy đồng mẫu số chung là $xyz$, ta có $ \frac{ayz + bxz + cxy}{xyz} = 0 $. Điều này suy ra tử số phải bằng 0, tức là $ ayz + bxz + cxy = 0 $ (với giả định $x, y, z \neq 0$ để các mẫu số xác định).
+ Thay thế và kết luận: Thay $ ayz + bxz + cxy = 0 $ vào biểu thức đã khai triển, ta được: $ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} + 2 \cdot \frac{0}{abc} = 1 $. Điều này đơn giản thành $ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} + 0 = 1 $, và cuối cùng là $ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 $

Các bài tập cùng chuyên đề
Với hai số a,b bất kì, thực hiện phép tính \(\left( {a + b} \right).\left( {a + b} \right)\).
Từ đó rút ra liên hệ giữa \({\left( {a + b} \right)^2}\) và \({a^2} + 2ab + {b^2}\)
- Khai triển \({\left( {2b + 1} \right)^2}\)
- Viết biểu thức \(9{y^2} + 6yx + {x^2}\) dưới dạng bình phương của một tổng.
Tính nhanh giá trị của biểu thức:
\({x^2} + \dfrac{1}{2}x + \dfrac{1}{{16}}\) tại x=99,75.
Chứng minh đẳng thức \({\left( {10a + 5} \right)^2} = 100a\left( {a + 1} \right) + 25\). Từ đó em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính \({25^2};{35^2}\).
Biểu thức \(25{x^2} + 20xy + 4{y^2}\) viết dưới dạng bình phương của một tổng là:
A. \({\left[ {5x + \left( { - 2y} \right)} \right]^2}\)
B. \({\left[ {2x + \left( { - 5y} \right)} \right]^2}\)
C. \({\left( {2x + 5y} \right)^2}\)
D. \({\left( {5x + 2y} \right)^2}\).
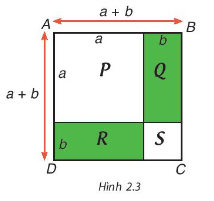
Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\).
Tính:
a) \({\left( {3x + 1} \right)^2}\)
b) \({\left( {4x + 5y} \right)^2}\)
c) \({\left( {5x - \dfrac{1}{2}} \right)^2}\)
d) \({\left( { - x + 2{y^2}} \right)^2}\)
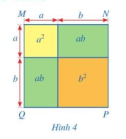
Diện tích của hình vuông MNPQ (hình 4) có thể được tính theo những cách nào?
Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \(\left( {a + b} \right)\left( {a + b} \right)\)
2. Hãy cho biết: \({\left( {a + b} \right)^2} = ?\)
Tính:
a) \({\left( {a + 4} \right)^2}\);
b) \({\left( {2u + 5v} \right)^2}\)
Viết các biểu thức sau dưới dạng bình phương của một tổng:
a) \(16{a^2} + 8a + 1\);
b) \({x^2} + 25{y^2} + 10xy\)
Tính nhanh: \( (0,76)^3 + (0,24)^3+3.0,76.0,24 \)
Biểu thức \({\left( {x - 2y} \right)^2}\) bằng:
A. \({x^2} + 2xy + 2{y^2}\)
B. \({x^2} - 2xy + 2{y^2}\)
C. \({x^2} + 4xy + 4{y^2}\)
D. \({x^2} - 4xy + 4{y^2}\)
a) Biết số tự nhiên a chia 3 dư 2. Chứng minh \({a^2}\) chia 3 dư 1.
b) Biết số tự nhiên a chia 5 dư 3. Chứng minh \({a^2}\) chia 5 dư 4.
Chứng minh rằng với mọi số tự nhiên n, ta có:
\({\left( {n + 2} \right)^2}\;-{n^2}\) chia hết cho 4.
Biết số tự nhiên a chia 3 dư 2. Chứng minh rằng \({a^2}\) chia 3 dư 1.
Biểu thức \({x^2} + x + \frac{1}{4}\) viết được dưới dạng bình phương của một tổng là
A.\({\left[ {x + \left( { - \frac{1}{2}} \right)} \right]^2}\).
B.\({\left( {x + \frac{1}{2}} \right)^2}\).
C.\({\left( {2x + \frac{1}{2}} \right)^2}\)
D.\({\left( {\frac{1}{2}x + 1} \right)^2}\)
Tính nhanh giá trị của biểu thức
\({x^2} + \frac{1}{2}x + \frac{1}{{16}}\) tại \(x = 99,75\).
Chứng minh đẳng thức \({\left( {10a + 5} \right)^2}\; = 100a\left( {a + 1} \right) + 25\). Từ đó, em hãy nêu một quy tắc tính nhẩm bình phương của một số có tận cùng là 5.
Áp dụng: Tính \({25^2},{35^2}\).
Biểu thức \(25{x^2}\; + 20xy + 4{y^2}\) viết dưới dạng bình phương của một tổng là:
A. \({\left[ {5x\; + \;\left( { - 2y} \right)} \right]^2}\).
B. \({\left[ {2x\; + \;\left( { - 5y} \right)} \right]^2}\).
C. \({\left( {2x + 5y} \right)^2}\).
D. \({\left( {5x + 2y} \right)^2}\).
Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2}\; = {a^2}\; + 2ab + {b^2}\).

Khai triển \((3x+2)^2\) ta được
-
A.
\(9x^2−12x+4\)
-
B.
\(3x^2+12x+4\)
-
C.
\(9x^2+12x+4\)
-
D.
\(3x^2+6x+4\)
Cho \({a^2} + {b^2} + {c^2} = ab + bc + ca\;\) và \(a + b + c = 2022\). Tính \(a, b, c\).
Chọn câu đúng:
-
A.
\({\left( {A + B} \right)^2} = {A^2} - 2AB + {B^2}\).
-
B.
\({\left( {A + B} \right)^2} = {A^2} + {B^2}\).
-
C.
\({\left( {A + B} \right)^2} = {A^2} + AB + {B^2}\).
-
D.
\({\left( {A + B} \right)^2} = {A^2} + 2AB + {B^2}\).
Khai triển \({\left( {3x + 4y} \right)^2}\), ta được:
-
A.
\(9{x^2} + 24xy + 16{y^2}\).
-
B.
\(9{x^2} + 24xy + 4{y^2}\).
-
C.
\(9{x^2} + 12xy + 16{y^2}\).
-
D.
\(9{x^2} + 6xy + 16{y^2}\).
Điền vào chỗ trống sau: \({\left( {x + 2} \right)^2} = {x^2} + ... + 4\)
-
A.
\(2x\).
-
B.
\(4x\).
-
C.
\(2\).
-
D.
\(4\).
Trong biểu thức \({\left( {2x + 5} \right)^2} = 4{x^2} + ... + 25\), đơn thức còn thiếu tại … là
-
A.
\(10x\).
-
B.
\( - 10x\).
-
C.
\(20x\).
-
D.
\( - 20x\).
Tính \({\left( {x + 3} \right)^2}\) ta được:
-
A.
\(\left( {x - 3} \right)\left( {x + 3} \right)\).
-
B.
\({x^2} - 6x + 3\).
-
C.
\({x^2} - 6x + 9\).
-
D.
\({x^2} + 6x + 9\).
Biểu thức thích hợp của đẳng thức \({x^2} + ... + 4{y^2} = {\left( {x + 2y} \right)^2}\) là:
-
A.
\(xy\).
-
B.
\(4xy\).
-
C.
\(2xy\).
-
D.
\( - 4xy\).
Biểu thức \({\left( {x + y} \right)^2}\) bằng biểu thức nào sau đây?
-
A.
\({x^2} - 2xy + {y^2}\).
-
B.
\({x^2} + {y^2}\).
-
C.
\({x^2} - {y^2}\).
-
D.
\({x^2} + 2xy + {y^2}\).