Giải các hệ phương trình sau bằng máy tính bỏ túi.
\(\left\{ \begin{array}{l}3,7x + 4,3y = - 2,5\\ - 5,1x + 2,7y = 4,8\end{array} \right.\)
Sử dụng máy tính cầm tay để tính nghiệm.
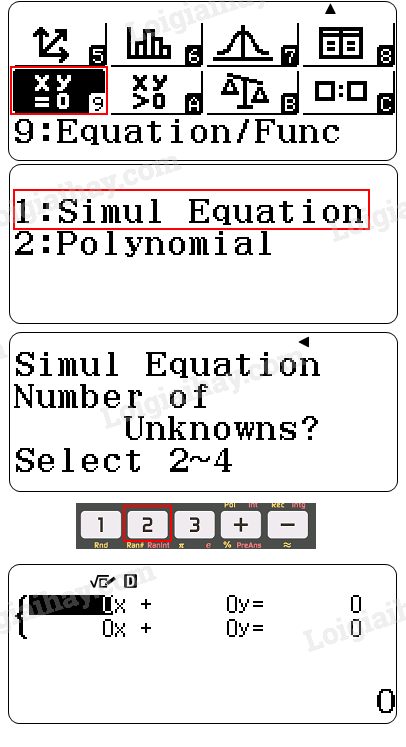
Tại giao diện nhập hệ phương trình, nhập các hệ số tương ứng của hai phương trình.
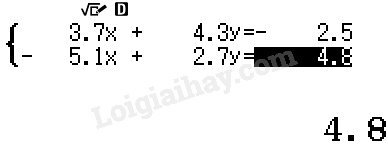
Bấm "=", ta được:

Bấm "=" tiếp

Ta được hai nghiệm \((x;y) = \left(-\frac{913}{1064};\frac{167}{1064}\right)\)
Nếu muốn đổi nghiệm về số thập phân, ta bấm nút: "S \(\Leftrightarrow\) D"
Nghiệm trở thành
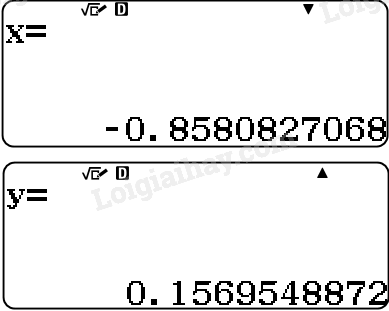
Ta được hai nghiệm \((x;y) \approx \left(-0,86;0,16\right)\)
Câu hỏi yêu cầu giải hệ phương trình $\left\{ \begin{array}{l}3,7x + 4,3y = - 2,5\\ - 5,1x + 2,7y = 4,8\end{array} \right.$ bằng máy tính bỏ túi. Hệ phương trình này là một hệ hai phương trình bậc nhất hai ẩn.
Để giải hệ này bằng máy tính, ta cần xác định các hệ số tương ứng: ${a_1} = 3,7$, ${b_1} = 4,3$, ${c_1} = -2,5$ cho phương trình thứ nhất và ${a_2} = -5,1$, ${b_2} = 2,7$, ${c_2} = 4,8$ cho phương trình thứ hai.
Phương pháp chung để giải hệ hai phương trình bậc nhất hai ẩn bằng máy tính cầm tay (MTCT) sử dụng chức năng giải hệ phương trình (thường có phím MODE/MENU).
Các bước thực hiện có thể khái quát như sau (ví dụ trên máy Fx-580VNX):
- Đưa hệ phương trình về dạng chuẩn: Đảm bảo hệ phương trình cần giải được viết dưới dạng $\left\{ \begin{array}{l}{a_1}x + {b_1}y = {c_1}\\{a_2}x + {b_2}y = {c_2}\end{array} \right.$. Chuyển các hằng số sang vế phải của mỗi phương trình nếu cần.
- Truy cập chức năng giải hệ phương trình: Nhấn phím MENU hoặc MODE, sau đó chọn tính năng giải phương trình/hệ phương trình (thường được ký hiệu là Equation/Func hoặc tương tự), rồi chọn chức năng giải hệ phương trình bậc nhất hai ẩn (thường ký hiệu là Simul Equation và chọn số lượng ẩn là 2).
- Nhập các hệ số: Nhập lần lượt các hệ số ${a_1}, {b_1}, {c_1}, {a_2}, {b_2}, {c_2}$ của hệ phương trình vào máy tính. Sau khi nhập mỗi hệ số, nhấn phím = để xác nhận và chuyển sang nhập hệ số tiếp theo.
- Xem kết quả: Sau khi nhập hết các hệ số, nhấn phím =. Màn hình sẽ hiển thị giá trị của $x$. Nhấn phím = lần nữa, màn hình sẽ hiển thị giá trị của $y$.
- Chuyển đổi dạng nghiệm (nếu cần): Nếu kết quả hiển thị dưới dạng phân số, có thể bấm nút "S $\Leftrightarrow$ D" để chuyển đổi sang dạng số thập phân gần đúng.
- Kiểm tra trường hợp đặc biệt: Máy tính cũng có thể báo các trường hợp đặc biệt: Infinite Solution (vô số nghiệm) hoặc No Solution (vô nghiệm).

Các bài tập cùng chuyên đề
Dùng MTCT thích hợp để tìm nghiệm của các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}2x + 3y = - 4\\ - 3x - 7y = 13;\end{array} \right.\)
b) \(\left\{ \begin{array}{l}2x + 3y = 1\\ - x - 1,5y = 1;\end{array} \right.\)
c) \(\left\{ \begin{array}{l}8x - 2y - 6 = 0\\4x - y - 3 = 0.\end{array} \right.\)
Thực hiện lần lượt các yêu cầu sau để tính số mililit dung dịch acid HCl nồng độ 20% và số mililit dung dịch acid HCl nồng độ 5% cần dùng để pha chế 2 lít dung dịch acid HCl nồng độ 10%.
a) Gọi x là số mililit dung dịch HCl nồng độ 20%, y là số mililit dung dịch HCl nồng độ 5% cần lấy. Hãy biểu thị qua x và y:
- Thể tích của dung dịch HCl 10% nhận được sau khi trộn lẫn hai dung dịch acid ban đầu.
- Tổng số gam acid HCl nguyên chất có trong hai dung dịch acid này.
b) Sử dụng kết quả ở câu a, hãy lập một hệ hai phương trình bậc nhất hai ẩn là x, y. Giải hệ phương trình này để tính số mililit cần lấy của mỗi dung dịch HCl ở trên.
Dùng MTCT thích hợp để tìm nghiệm của các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}12x - 5y + 24 = 0\\ - 5x - 3y - 10 = 0;\end{array} \right.\)
b) \(\left\{ \begin{array}{l}\frac{1}{3}x - y = \frac{2}{3}\\x - 3y = 2;\end{array} \right.\)
c) \(\left\{ \begin{array}{l}3x - 2y = 1\\ - x + \frac{2}{3}y = 0;\end{array} \right.\)
d) \(\left\{ \begin{array}{l}\frac{4}{9}x - \frac{3}{5}y = 11\\\frac{2}{9}x + \frac{1}{5}y = - 2.\end{array} \right.\)
Cặp số nào sau đây là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}5x + 7y = - 1\\3x + 2y = - 5\end{array} \right.?\)
A. \(\left( { - 1;1} \right).\)
B. \(\left( { - 3;2} \right).\)
C. \(\left( {2; - 3} \right).\)
D. \(\left( {5;5} \right).\)
Hệ phương trình \(\left\{ \begin{array}{l}1,5x - 0,6y = 0,3\\ - 2x + y = - 2\end{array} \right.\)
A. Có nghiệm là \(\left( {0; - 0,5} \right).\)
B. Có nghiệm là \(\left( {1;0} \right).\)
C. Có nghiệm là \(\left( { - 3; - 8} \right).\)
D. Vô nghiệm.
Hệ phương trình \(\left\{ \begin{array}{l}0,6x + 0,3y = 1,8\\2x + y = - 6\end{array} \right.\)
A. Có 1 nghiệm.
B. Vô nghiệm.
C. Có vô số nghiệm.
D. Có hai nghiệm.
Tìm nghiệm của các hệ phương trình sau bằng máy tính cầm tay:
a) \(\left\{ {\begin{array}{*{20}{c}}{2x - y = 4}\\{3x + 5y = - 19}\end{array}} \right.\)
b) \(\left\{ {\begin{array}{*{20}{c}}{ - 3x + 5y = 12}\\{2x + y = 5}\end{array}} \right.\)
Sử dụng máy tính cầm tay để tìm nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}3x - 2y = 1\\ - 6x + y = 3\end{array} \right.\)
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x + y = 9\\x - y = - 1\end{array} \right.\) là:
A. \(\left( {x;y} \right) = \left( {4,5} \right)\);
B. \(\left( {x;y} \right) = \left( {5;4} \right)\);
C. \(\left( {x;y} \right) = \left( { - 5; - 4} \right)\);
D. \(\left( {x;y} \right) = \left( { - 4; - 5} \right)\)
Sử dụng máy tính cầm tay thích hợp, tìm nghiệm của các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}9x - 5y = - 11\\22x + 17y = 3;\end{array} \right.\)
b) \(\left\{ \begin{array}{l}\frac{2}{5}x - \frac{3}{8}y = \frac{1}{4}\\ - \frac{4}{5}x + \frac{9}{8}y = \frac{7}{8}\end{array} \right.\)
c) \(\left\{ \begin{array}{l}0,6x - 0,7y = 1,5\\ - 0,2x + 0,3y = - 1\end{array} \right.\)
Sử dụng máy tính cầm tay thích hợp, tìm nghiệm của mỗi hệ phương trình sau:
a) \(\left\{ \begin{array}{l}11x - 13y = - 7\\7x + 19y = 2\end{array} \right.\)
b) \(\left\{ \begin{array}{l}\frac{1}{8}x + \frac{3}{4}y = \frac{1}{{16}}\\ - \frac{4}{5}x + \frac{7}{5}y = \frac{1}{5}\end{array} \right.\)
c) \(\left\{ \begin{array}{l}0,12x - 0,15y = - 2,4\\0,21x + 0,35y = - 3,6\end{array} \right.\)
(Sử dụng máy tính cầm tay) Hệ phương trình \(\left\{ \begin{array}{l}3x - 2y = 1\\x + 5y = 6\end{array} \right.\) có nghiệm là
-
A.
\(\left( { - 1; - 1} \right)\).
-
B.
\(\left( { - 1;1} \right)\).
-
C.
\(\left( {1; - 1} \right)\).
-
D.
\(\left( {1;1} \right)\).
(Sử dụng máy tính cầm tay) Hệ phương trình \(\left\{ \begin{array}{l}x - 2y = 3\\ - 2x + 4y = 11\end{array} \right.\) có nghiệm là
-
A.
\(\left( { - 1;1} \right)\).
-
B.
\(\left( { - 5;\frac{1}{4}} \right)\).
-
C.
vô nghiệm.
-
D.
vô số nghiệm.
(Sử dụng máy tính cầm tay) Hệ phương trình \(\left\{ \begin{array}{l}x + 3y = 2\\3x + 9y = 6\end{array} \right.\) có
-
A.
một nghiệm duy nhất.
-
B.
hai nghiệm.
-
C.
vô nghiệm.
-
D.
vô số nghiệm.
(Sử dụng máy tính cầm tay) Hệ phương trình \(\left\{ \begin{array}{l}6x + 1 = y\\ - 5x + 2y = - 12\end{array} \right.\) có nghiệm là
-
A.
\(\left( { - 2; - 11} \right)\).
-
B.
\(\left( { - 11; - 2} \right)\).
-
C.
\(\left( {2;11} \right)\).
-
D.
\(\left( {11;2} \right)\).
(Sử dụng máy tính cầm tay) Hệ phương trình \(\left\{ \begin{array}{l}2\left( {x + y} \right) + 3\left( {x - y} \right) = 4\\\left( {x + y} \right) + 2\left( {x - y} \right) = 5\end{array} \right.\) có nghiệm là
-
A.
\(\left( { - 7;6} \right)\).
-
B.
\(\left( {6; - 7} \right)\).
-
C.
\(\left( { - \frac{1}{2}; - \frac{{13}}{2}} \right)\).
-
D.
\(\left( {\frac{{13}}{2};\frac{1}{2}} \right)\).
Hệ phương trình \(\left\{ \begin{array}{l}\frac{5}{3}x + y = - 2\\x - y = 3\end{array} \right.\)
A. có nghiệm là \(\left( {\frac{3}{8};\frac{{27}}{8}} \right)\).
B. có nghiệm là \(\left( {\frac{3}{8};\frac{{ - 21}}{8}} \right)\).
C. vô nghiệm.
D. có nghiệm là \(\left( {\frac{{ - 3}}{8};\frac{{27}}{8}} \right)\).
Hệ phương trình \(\left\{ \begin{array}{l} - 2,5x + y = 5\\0,5x - 1,5y = 0\end{array} \right.\)
A. có một nghiệm.
B. có hai nghiệm.
C. vô nghiệm.
D. có vô số nghiệm.
Dùng MTCT thích hợp để tìm nghiệm của các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}12x - 5y + 24 = 0\\ - 5x - 3y - 10 = 0\end{array} \right.\);
b) \(\left\{ \begin{array}{l}\frac{1}{3}x - y = \frac{2}{3}\\x - 3y = 2\end{array} \right.\);
c) \(\left\{ \begin{array}{l}3x - 2y = 1\\ - x + \frac{2}{3}y = 0\end{array} \right.\);
d) \(\left\{ \begin{array}{l}\frac{4}{9}x - \frac{3}{5}y = 11\\\frac{2}{9}x + \frac{1}{5}y = - 2\end{array} \right.\).
Nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x + 3y = - 1\\2x - y = 7\end{array} \right.\) là
A. (-1; 1).
B. (3; -1).
C. \(\left( {\frac{1}{2}; - 1} \right)\).
D. (2; -3).
Hệ phương trình nào sau đây có nghiệm duy nhất?
A. \(\left\{ \begin{array}{l}x - 2y = 3\\2x - 4y = 5\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - 2y = 3\\ - 2x + 4y = - 6\end{array} \right.\).
C. \(\left\{ \begin{array}{l}x - 2y = 3\\2x + 4y = 5\end{array} \right.\).
D. \(\left\{ \begin{array}{l}x - 2y = 3\\ - x + 2y = - 2\end{array} \right.\).
Sử dụng MTCT, tìm nghiệm của các hệ phương trình sau:
a) \(\left\{ \begin{array}{l}\sqrt 3 x + 3y = 1\\2x - \sqrt 3 y = \sqrt 3 \end{array} \right.\);
b) \(\left\{ \begin{array}{l}2,5x - 3,5y = 0,5\\ - 0,5x + 0,7y = 1\end{array} \right.\);
c) \(\left\{ \begin{array}{l}\frac{x}{5} + \frac{y}{2} = 5\\0,4x + y = 1\end{array} \right.\).
Hệ phương trình \(\left\{ \begin{array}{l}1,5x - 0,6y = 0,3\\ - 2x + y = - 2\end{array} \right.\)
A. có nghiệm là (0; -0,5).
B. có nghiệm là (1; 0).
C. có nghiệm là (-3; -8).
D. vô nghiệm.
Hệ phương trình \(\left\{ \begin{array}{l}0,6x + 0,3y = 1,8\\2x + y = - 6\end{array} \right.\)
A. có một nghiệm.
B. vô nghiệm.
C. có vô số nghiệm.
D. có hai nghiệm.
Với m = 2, hệ phương trình \(\left\{ \begin{array}{l}2mx + 5y = 23\\3x + 3y = 15\end{array} \right.\) có cặp nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\) thỏa mãn biểu thức \(P = \frac{{{x_0}^2 + 4}}{{{y_0} + 5}} + 2024\). Tính giá trị của P.
Cho hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{4x - y = 2}\\{x + 3y = 7}\end{array}} \right.\) . Cặp số nào dưới đây là nghiệm của hệ phương trình đã cho?
-
A.
\(\left( {2;2} \right)\).
-
B.
\(\left( { - 1; - 2} \right)\).
-
C.
\(\left( {1;2} \right)\).
-
D.
\(\left( {2; - 2} \right)\).
-
A.
\(\left( {1; - 1} \right)\)
-
B.
\(\left( { - 1;1} \right)\)
-
C.
\(\left( {1;1} \right)\)
-
D.
\(\left( { - 1; - 1} \right)\)







Danh sách bình luận