Cho tam giác MNP vuông tại M. Lấy I là trung điểm của MP.
a) Chứng minh: NM < NI < NP.
b) Trên tia đối của tia IN lấy điểm K sao cho IK = IN. Chứng minh MN = PK từ đó suy ra PK < NP.
c) So sánh \(\widehat {MNI}\) và \(\widehat {INP}\).
d) Từ I kẻ IH\( \bot \)NP. So sánh IM và IH.
a) Sử dụng tính chất của trung điểm và quan hệ giữa đường vuông góc và đường xiên để chứng minh.
b) Chứng minh \(\Delta IMN = \Delta IPK\) suy ra MN = PK.
Trong tam giác vuông thì cạnh huyền là cạnh lớn nhất nên MN < NP. Kết hợp suy ra PK < NP.
c) Sử dụng quan hệ giữa góc và cạnh đối diện để so sánh.
d) Sử dụng quan hệ giữa đường vuông góc và đường xiên và tính chất của trung điểm để so sánh.
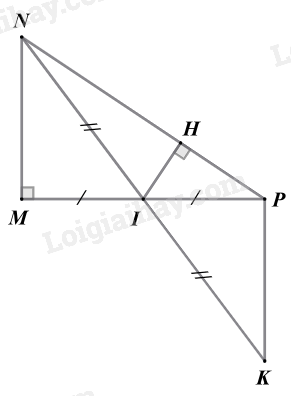
a) Vì I là trung điểm của MP nên MI < MP.
Mà \(NM \bot MP\) (\(\Delta MNP\) vuông tại M)
suy ra \(NM < NI < NP\) (quan hệ giữa đường vuông góc và đường xiên)
b) Xét \(\Delta IMN\) và \(\Delta IPK\) có:
\(IM = IP\) (I là trung điểm của MP)
\(\widehat {MIN} = \widehat {PIK}\)
\(IN = IK\) (gt)
Suy ra \(\Delta IMN = \Delta IPK\) (c.g.c)
Do đó MN = PK.
Tam giác MNP vuông tại M nên MN < NP, suy ra PK < NP.
c) Vì \(\Delta IMN = \Delta IPK\) nên \(\widehat {INM} = \widehat {IKP}\).
Vì \(KP < NP\) nên \(\widehat {PNK} < \widehat {PKN}\) (góc đối diện với cạnh), suy ra \(\widehat {INP} < \widehat {INM}\).
d) Vì \(IH \bot NP\) nên \(IH < IP\) (quan hệ giữa đường vuông góc và đường xiên)
Mà IM = IP nên \(IH < IM\).
Các bài tập cùng chuyên đề
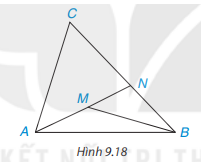
Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC. (H.9.18)
a) So sánh MB với MN + NB, từ đó suy ra MA + MB < NA + NB
b) So sánh NA với CA + CN, từ đó suy ra NA + NB < CA + CB
c) Chứng minh MA + MB < CA + CB.
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng
a) \(AI < \dfrac{1}{2}\left( {AB + AC} \right)\)
b) \(AM < \dfrac{1}{2}\left( {AB + AC} \right)\)
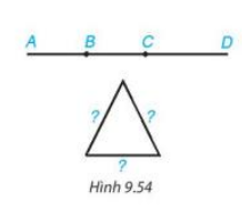
Một sợ dây thép dài 1,2m. Cần đánh dấu trên sợ dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành tam giác cân có một cạnh bằng 30 cm (h.9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.
Cho tam giác ABC có: \(\widehat A = 42^\circ ,\widehat B = 37^\circ \).
a) Tính \(\widehat C\).
b) So sánh độ dài các cạnh AB, BC, CA.
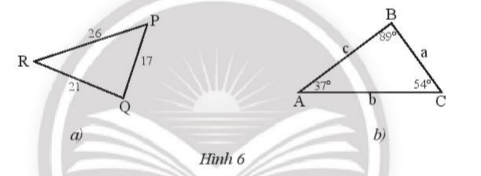
a) Sắp xếp theo thứ tự từ nhỏ đến lớn số đo các góc của tam giác PQR hinh 6a.
b) Sắp xếp theo thứ tự từ nhỏ đến lớn độ dài các cạnh của tam giác ABC ở hình 6b.
a) Cho tam giác DEF có góc F là góc tù. Theo em, cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác DEF.
b) Cho tam giác ABC vuông tại A. Theo em, cạnh nào là cạnh có độ dài lớn nhất trong ba cạnh của tam giác ABC?
a) Cho tam giác ABC có AB = 15 cm, BC = 8 cm. Tính độ dài cạnh AC, biết độ dài của nó (theo đơn vị xăng-ti-mét) là một số nguyên tố lớn hơn bình phương của 4.
b) Độ dài ba cạnh của tam giác MNP tỉ lệ với 2; 3; 4. Tính độ dài cạnh lớn nhất, biết tổng độ dài hai cạnh còn lại là 20 cm.
Tam giác ABC có AB = 2cm, BC = 3cm. Đặt CA = b (cm)
a) Chứng minh rằng 1 < b < 5
b) Giả sử rằng với 1 < b < 5, có tam giác ABC thoả mãn AB = 2cm, BC = 3 cm, CA = b (cm). Với mỗi tam giác đó, hãy sắp xếp ba góc A, B, C theo thứ tự từ bé đến lớn.
