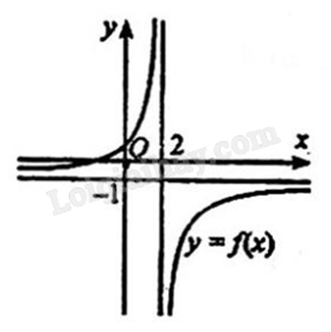
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\), \((c \ne 0,ad - bc \ne 0)\) có đồ thị như hình bên. Tiệm cận đứng của đồ thị hàm số đã cho là
-
A.
y = -1
-
B.
y = 2
-
C.
x = -1
-
D.
x = 2
Quan sát đồ thị và nhận xét.
Tiệm cận đứng của đồ thị hàm số đã cho là x = 2.
Đáp án : D

Các bài tập cùng chuyên đề
Để loại bỏ p% một loài tảo độc khỏi hồ nước, người ta ước tính chi phí bỏ ra là \(C\left( p \right) = \frac{{45p}}{{100 - p}}\) (triệu đồng), với \(0 \le p < 100\). Tìm tiệm cận đứng của đồ thị hàm số C(p) và nêu ý nghĩa của đường tiệm cận này.
Cho hàm số \(y = f\left( x \right) = \frac{x}{{x - 1}}\) có đồ thị (C). Với \(x > 1\), xét điểm M (x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng \(x = 1\) (H.1.22).

a) Tính khoảng cách MH.
b) Khi M thay đổi trên (C) sao cho khoảng cách MH dần đến 0, có nhận xét gì về tung độ của điểm M?
Đường thẳng \(x = 1\) có phải là tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 2x - 3}}{{x - 1}}\) không?
Tìm tiệm cận đứng của đồ thị hàm số \(y = \frac{{{x^2} + 3x}}{{x - 5}}\).
Cho hàm số \(y = f\left( x \right) = \frac{1}{x}\) có đồ thị là đường cong như Hình 12. Tìm \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right)\)

Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x + 2}}{{x + 1}}\) là:
A. \(x = - 1\).
B. \(x = - 2\).
C. \(x = 1\).
D. \(x = 2\).
Tìm tiệm cận đứng của đồ thị các hàm số sau:
a) \(f(x) = \frac{{2x + 3}}{{ - x + 5}}\)
b) \(g(x) = \frac{{{x^2} - 2x}}{{x - 1}}\)
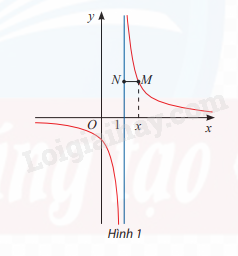
Cho hàm số \(y = \frac{1}{{x - 1}}\)có đồ thị như Hình 1.
a) Tìm \(\mathop {\lim }\limits_{x \to {1^ + }} = \frac{1}{{x - 1}},\mathop {\lim }\limits_{x \to {1^ - }} = \frac{1}{{x - 1}}\)
b) Gọi M là điểm trên đồ thị có hoành độ x. Đường thẳng đi qua M và vuông góc với trục Oy cắt đường thẳng x = 1 tại điểm N. Tính MN theo x và nhận xét về MN khi \(x \to {1^ + }\) và \(x \to {1^ - }\)
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{ - 2x + 3}}{{5x + 1}}\) là đường thẳng có phương trình
A. \(y = - \frac{1}{5}\)
B. \(y = - \frac{2}{5}\)
C. \(x = - \frac{1}{5}\)
D. \(x = - \frac{2}{5}\)
Đồ thị \(y = \frac{{{x^2} - 3x + 2}}{{x - 1}}\) có tất cả bao nhiêu đường tiệm cận đứng?
-
A.
3
-
B.
1
-
C.
0
-
D.
2
Khoảng cách từ điểm A(-5;1) đến đường tiệm cận đứng của đồ thị hàm số \(y = \frac{{\sqrt {1 - {x^2}} }}{{{x^2} + 2x}}\) là bao nhiêu?
Với giá trị nào của tham số m để đồ thị hàm số \(y = \frac{{m{x^2} - 4}}{{mx - 1}}\) có tiệm cận đứng đi qua điểm A(1;4)?
Với giá trị nào của tham số m để đồ thị hàm số \(y = \frac{{3x - 1}}{{2x - m}}\) có tiệm cận đứng đi qua điểm A(1;3)?
Cho hàm số \(y = f\left( x \right) = \frac{{{x^2} + 3x - 10}}{{x - 2}}\). Đồ thị hàm số \(f\left( x \right)\) có tiệm cận đứng không?
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{3{\rm{x}} + 1}}{{x - 2}}\) là đường thẳng:
A. \(x = 2\).
B. \(x = - \frac{1}{3}\).
C. \(y = 3\).
D. \(y = \frac{1}{3}\).
Đồ thị hàm số nào sau đây nhận đường thẳng \(x = - 1\) làm tiệm cận đứng?
A. \(y = \frac{{3{\rm{x}} - 1}}{{{\rm{x}} + 1}}\).
B. \(y = \frac{{2{\rm{x}} + 1}}{{{\rm{x}} - 1}}\).
C. \(y = \frac{{ - x + 1}}{{{\rm{x}} - 2}}\).
D. \(y = \frac{{x + 1}}{{{\rm{x}} - 2}}\).
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
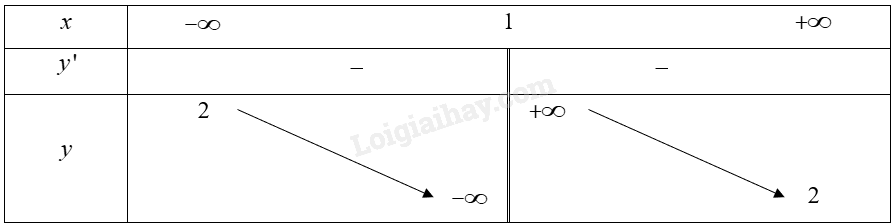
Tiệm cận đứng của đồ thị hàm số là đường thẳng:
A. \(x = 1\).
B. \(x = 2\).
C. \(y = 1\).
D. \(y = 2\).
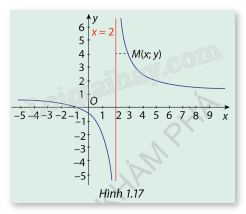
Cho hàm số \(y = \frac{{x + 1}}{{x - 2}}\)có đồ thị (C ) như Hình 1.17.
a) Nêu nhận xét về khoảng cách từ điểm \(M(x;y) \in (C)\)đến đường thẳng x = 2 khi \(x \to 2\) .
b) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {2^ + }} f(x)\) và \(\mathop {\lim }\limits_{x \to {2^ - }} f(x)\).
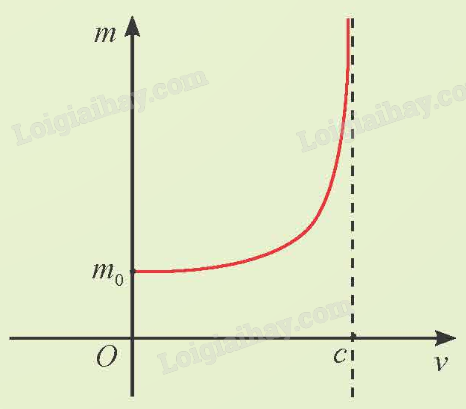
Trong phần Khởi động đầu bài, tìm đường tiệm cận đứng của đồ thị hàm số \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), từ đó nhận xét khối lượng của vật khi vận tốc của nó càng gần vận tốc ánh sáng.
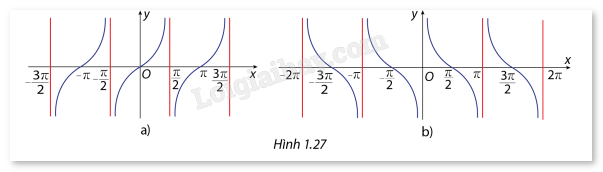
Xác định các đường tiệm cận đứng của các đồ thị hàm số \(y = \tan x\) ( hình 1.27a) và \(y = \cot x\) (hình 1.27b).
Tổng số đường tiệm cận đứng của đồ thị hàm số \(\frac{1}{{4 - {x^2}}}\) là
-
A.
0
-
B.
1
-
C.
2
-
D.
3
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{x - 1}}{{x - 3}}\) là
-
A.
\(x = - 3\)
-
B.
\(x = - 1\)
-
C.
\(x = 1\)
-
D.
\(x = 3\)
Cho hàm số y = f(x) có bảng biến thiên như sau:
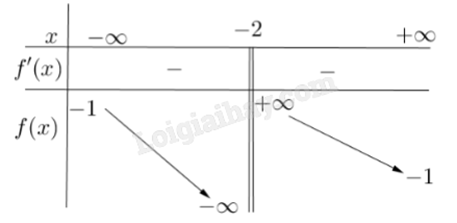
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
-
A.
x = -1
-
B.
y = -1
-
C.
y = -2
-
D.
x = -2
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{3x + 2}}{{x - 2}}\) là đường thẳng có phương trình
-
A.
x = 2
-
B.
x = -1
-
C.
x = 3
-
D.
x = -2
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) \((ad - bc \ne 0;c \ne 0)\) có bảng biến thiên như sau:
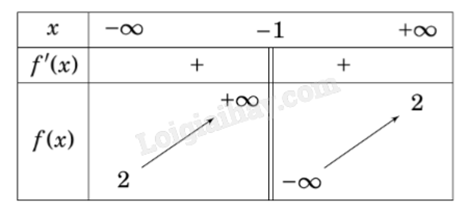
Đồ thị hàm số có đường tiệm cận đứng là
-
A.
y = 2
-
B.
y = -1
-
C.
x = 2
-
D.
x = -1
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận đứng?
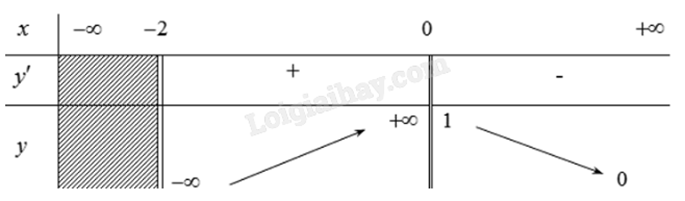
-
A.
3
-
B.
2
-
C.
4
-
D.
1
Cho hàm số y = f(x) có bảng biến thiên như sau:
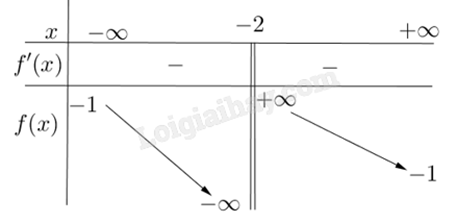
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình
-
A.
x = -1
-
B.
x = -2
-
C.
y = -1
-
D.
y = -2
Cho hàm số $y=\frac{ax+b}{cx+d}$ $(c\ne 0,ad-bc\ne 0)$ có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số là
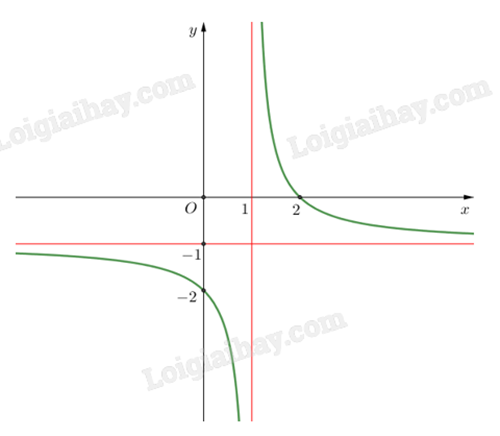
-
A.
x = -1
-
B.
y = -1
-
C.
x = 1
-
D.
y = 1
Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \(m = m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\), trong đó \({m_0}\) là khối lượng nghỉ của hạt c = 300 000 km/s là tốc độ ánh sáng. Khi hạt di chuyển với tốc độ càng gần tốc độ ánh sáng thì khối lượng của hạt thay đổi như thế nào? Điều này thể hiện trên đồ thị hàm số m = m(v) ở hình bên như thế nào?
Cho hàm số $y = \dfrac{ax + b}{cx + d}$ ($ac \neq 0$, $ad - bc \neq 0$) có đồ thị như hình bên. Đường tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
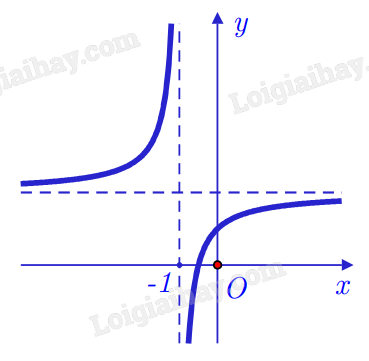
-
A.
$y = - 1$.
-
B.
$x = - 1$.
-
C.
$y = 2$.
-
D.
$x = 2$.







Danh sách bình luận