Một chiếc đèn trang trí (gồm các bóng đèn gắn vào một giá hình tròn) như hình bên dưới. Đèn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên giá sao cho tam giác ABC đều. Độ dài của ba đoạn dây OA, OB, OC đều bằng L, trọng lượng của chiếc đèn là 27 N, bán kính của giá hình tròn là 0,5 m.

Biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là 12 N . Hỏi chiều dài tối thiểu của mỗi sợi dây là bao nhiêu mét (kết quả làm tròn đến hàng phần trăm)?
Đáp án:
Đáp án:
Áp dụng quy tắc tổng hợp lực, tính chất vecto của trọng tâm tam giác.
Gọi G là trọng tâm tam giác ABC. Vì tam giác ABC đều nên G là tâm đường tròn ngoại tiếp tam giác ABC . Do đó, GA = GB = GC = 0,5 m.
Theo đề bài, ta có OA = OB = OC = L nên \(OG \bot (ABC)\) và \(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = L\).
Gọi F là độ lớn của các lực căng \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) trên mỗi sợi dây. Khi đó, F = F(L) là một hàm số với biến số L.
Ta có \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = F\) và tồn tại hằng số \(k \ne 0\) sao cho \(\overrightarrow {{F_1}} = k\overrightarrow {OA} \), \(\overrightarrow {{F_2}} = k\overrightarrow {OB} \), \(\overrightarrow {{F_3}} = k\overrightarrow {OC} \).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = k\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = k.3\overrightarrow {OG} \).
Mặt khác, có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \) với \(\overrightarrow P \) là trọng lực tác dụng lên chiếc đèn.
Suy ra \(\left| {\overrightarrow P } \right| = 27 \Rightarrow k.3\left| {\overrightarrow {OG} } \right| = 27 \Leftrightarrow k = \frac{9}{{OG}}\).
Tam giác AOG vuông tại G nên \(OG = \sqrt {O{A^2} - G{A^2}} = \sqrt {{L^2} - 0,{5^2}} \) với L > 0,5.
Khi đó \(F(L) = \left| {\overrightarrow {{F_1}} } \right| = k\left| {\overrightarrow {OA} } \right| = \frac{{9L}}{{\sqrt {{L^2} - 0,{5^2}} }}\) (với L > 0,5).
Suy ra \(F(L) \le 12 \Leftrightarrow \frac{{9L}}{{\sqrt {{L^2} - 0,{5^2}} }} \le 12 \Leftrightarrow 3L \le 4\sqrt {{L^2} - 0,{5^2}} \)
\(\Leftrightarrow 9{L^2} \le 16{L^2} - 4 \Leftrightarrow 7{L^2} \ge 4 \Leftrightarrow L \ge \frac{{2\sqrt 7 }}{7}\).
Vậy chiều dài tối thiểu của mỗi sợi dây là \(\frac{{2\sqrt 7 }}{7} \approx 0,76\) (m).

Các bài tập cùng chuyên đề
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB\). Chứng minh rằng \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \).
Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right)\) và \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right)\).

Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó:
a) \(\overrightarrow {AA'} \) và \(\overrightarrow {C'C;} \)
b) \(\overrightarrow {AA'} \) và \(\overrightarrow {BC;} \)
c) \(\overrightarrow {AC} \) và \(\overrightarrow {B'A'} \).
Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho \(SM = 2AM\). Trên cạnh BC, lấy điểm N sao cho \(CN = 2BN\). Chứng minh rằng \(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \).
Cho tứ diện ABCD. Lấy G là trọng tâm của tam giác BCD. Khẳng định nào sau đây là sai?
A. \(\overrightarrow {BG} + \overrightarrow {CG} + \overrightarrow {DG} = \overrightarrow 0 \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
C. \(\overrightarrow {BC} + \overrightarrow {BD} = 3\overrightarrow {BG} \).
D. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Cho hình hộp ABCD.A’B’C’D’. Lấy M là trung điểm của đoạn thẳng CC’. Vectơ \(\overrightarrow {AM} \) bằng
A. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
B. \(\overrightarrow {AB} + \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AA'} \).
C. \(\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AA'} \).
D. \(\frac{1}{2}\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào dưới đây là sai?
A. \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AB'} \).
B. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
C. \(\overrightarrow {AD} + \overrightarrow {BB'} = \overrightarrow {AD'} \).
D. \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AC'} \).
Cho hình hộp ABCD.A’B’C’D’, gọi G là trọng tâm của tam giác BDA’.
a) Biểu diễn \(\overrightarrow {AG} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} \) và \(\overrightarrow {AA'} \).
b) Từ câu a, hãy chứng tỏ ba điểm A, G và C’ thẳng hàng.
Cho tứ diện ABCD, chứng minh rằng:
a) \(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\);
b) Nếu \(AB \bot CD\) và \(AC \bot BD\) thì \(AD \bot BC\).
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi G là trọng tâm của tam giác BC’D’.
a) Chứng minh rằng \(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\).
b) Tính theo a độ dài đoạn thẳng AG.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi G là trọng tâm của tam giác BC’D’.
a) Chứng minh rằng \(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\).
b) Tính theo a độ dài đoạn thẳng AG.
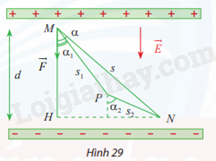
Một lực tĩnh điện \(\overrightarrow F \) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình 29). Biết \(q = {2.10^{ - 12}}C\), vectơ điện trường có độ lớn \(E = 1,{8.10^5}\)N/C và d = MH = 5mm. Tính công A sinh bởi lực tĩnh điện \(\overrightarrow F \).
Phát biểu nào sau đây là đúng?
-
A.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - \overrightarrow b \)
-
B.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \)
-
C.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a \overrightarrow b \)
-
D.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b \)
Cho hình hộp ABCD.A’B’C’D’.
a) Các vecto bằng với vecto \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ,\overrightarrow {D'C'} ,\overrightarrow {A'B'} \)
b) Vecto đối của vecto \(\overrightarrow {A'A} \) là \(\overrightarrow {B'B} \)
c) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {A'B'} \)
d) \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {C'A} \)
Trong không gian cho điểm O và bốn điểm A, B, C, D không thẳng hàng. Điều kiện cần và đủ để A, B, C, D tạo thành hình bình hành là?
-
A.
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
-
B.
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
-
C.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} = \overrightarrow {OC} + \frac{1}{2}\overrightarrow {OD} \)
-
D.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OC} = \overrightarrow {OB} + \frac{1}{2}\overrightarrow {OD} \)
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Xét các vecto \(\overrightarrow x = 2\overrightarrow a - \overrightarrow b \); \(\overrightarrow y = - 4\overrightarrow a + 2\overrightarrow b \); \(\overrightarrow z = - 3\overrightarrow b - 2\overrightarrow c \). Chọn khẳng định đúng?
-
A.
Hai vecto \(\overrightarrow y ,\overrightarrow z \) cùng phương
-
B.
Hai vecto \(\overrightarrow x ,\overrightarrow y \) cùng phương
-
C.
Hai vecto \(\overrightarrow x ,\overrightarrow z \) cùng phương
-
D.
Ba vecto \(\overrightarrow x ,\overrightarrow y ,\overrightarrow z \) đồng phẳng.
Cho hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có \(AB = a\), \(BC = 2a\), \(A{A_1} = 3a\).
a) \(\left( {\overrightarrow {A{B_1}} ;\overrightarrow {{C_1}D} } \right) = {45^o}\)
b) \(\overrightarrow {{A_1}B} .\overrightarrow {{D_1}D} = 9{a^2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {{C_1}{A_1}} .\overrightarrow {{C_1}{B_1}} \)
d) \(\overrightarrow {{A_1}{D_1}} .\overrightarrow {{C_1}C} = 0\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và G là trọng tâm tam giác SBD.
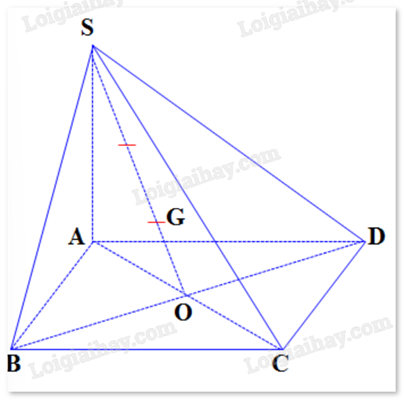
a) \(\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} \)
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \)
c) \(\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} \)
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Vecto trong không gian là một đoạn thẳng có hướng
-
B.
Hai vecto cùng phương là hai vecto có giá song song hoặc trùng nhau
-
C.
Hai vecto bằng nhau là hai vecto cùng hướng và có độ dài bằng nhau
-
D.
Hai vecto cùng phương thì cùng hướng
Cho hình hộp ABCD.A’B’C’D’.
a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'} \)
b) \(\overrightarrow {BD} + \overrightarrow {DD'} + \overrightarrow {B'D'} = \overrightarrow {BB'} \)
c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0 \)
d) \(\overrightarrow {AB'} = \overrightarrow {C'D} \)
Cho hình hộp ABCD.A’B’C’D’.
a) \(\overrightarrow {A'A} = - \overrightarrow {CC'} \)
b) \(\overrightarrow {BA'} = \overrightarrow {CD'} \)
c) \(\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} = \overrightarrow {A'C} \)
d) \(\overrightarrow {C'C} + \overrightarrow {AB} + \overrightarrow {B'C'} = 2\overrightarrow {A'C} \)
Cho tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = \widehat {BAD} = {60^o}\). Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \).
-
A.
\({60^o}\)
-
B.
\({45^o}\)
-
C.
\({120^o}\)
-
D.
\({90^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\) và \(\overrightarrow a .\overrightarrow b = 3\). Độ dài vecto \(3\overrightarrow a + 5\overrightarrow b \) là?
-
A.
\(5\sqrt 5 \)
-
B.
\(\sqrt {124} \)
-
C.
8
-
D.
124
Cho hình chóp S.ABCD.
a) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
b) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {CD} \)
c) Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành
d) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Nếu \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng thì từ \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) ta suy ra m = n = p = 0
-
B.
Nếu có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \), trong đó \({m^2} + {n^2} + {p^2} > 0\) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
C.
Với ba số thực m, n, p thỏa mãn \(m + n + p \ne 0\) ta có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
D.
Nếu giá của \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng quy thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
Cho tứ diện hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN,SC) bằng
-
A.
\({45^o}\)
-
B.
\({30^o}\)
-
C.
\({90^o}\)
-
D.
\({60^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \ne 0\). Xác định góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\).
-
A.
\(\alpha = {180^o}\)
-
B.
\(\alpha = {0^o}\)
-
C.
\(\alpha = {90^o}\)
-
D.
\(\alpha = {45^o}\)
Cho tứ diện ABCD có các cạnh đều bằng a.
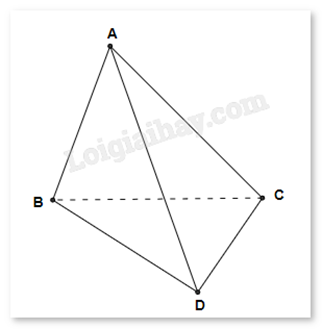
a) \(\overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \)
d) \(AB \bot CD\)
Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Vì I là trung điểm đoạn AB nên từ O bất kì ta có: \(\overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
-
B.
Vì \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \) nên bốn điểm A, B, C, D đồng phẳng
-
C.
Vì \(\overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow 0 \) nên N là trung điểm của đoạn NP
-
D.
Từ hệ thức \(\overrightarrow {AB} = 2\overrightarrow {AC} - 8\overrightarrow {AD} \) ta suy ra ba vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) đồng phẳng
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)






