Cho hình hộp ABCD.A’B’C’D’.
a) Các vecto bằng với vecto \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ,\overrightarrow {D'C'} ,\overrightarrow {A'B'} \)
b) Vecto đối của vecto \(\overrightarrow {A'A} \) là \(\overrightarrow {B'B} \)
c) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {A'B'} \)
d) \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {C'A} \)
a) Các vecto bằng với vecto \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ,\overrightarrow {D'C'} ,\overrightarrow {A'B'} \)
b) Vecto đối của vecto \(\overrightarrow {A'A} \) là \(\overrightarrow {B'B} \)
c) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {A'B'} \)
d) \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {C'A} \)
Sử dụng các quy tắc cộng, trừ vecto và lý thuyết các vecto bằng nhau, các vecto đối nhau.
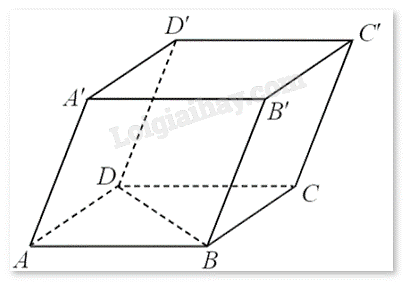
a) Đúng. Các vecto bằng với vecto \(\overrightarrow {AB} \) là \(\overrightarrow {DC} ,\overrightarrow {D'C'} ,\overrightarrow {A'B'} \) vì chúng cùng phương, cùng chiều và cùng độ dài.
b) Sai. Hai vecto \(\overrightarrow {A'A} \),\(\overrightarrow {B'B} \) cùng chiều nên không phải vecto đối nhau.
c) Đúng. Vì \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {AB} = 2\overrightarrow {A'B'} \).
d) Sai. Vì \(\overrightarrow {BB'} - \overrightarrow {CA} = \overrightarrow {CC'} - \overrightarrow {CA} = \overrightarrow {AC'} \).

Các bài tập cùng chuyên đề
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho \(SE = \frac{1}{3}SA,SF = \frac{1}{3}SB\). Chứng minh rằng \(\overrightarrow {EF} = \frac{1}{3}\overrightarrow {DC} \).
Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc \(\left( {\overrightarrow {AA'} ,\overrightarrow {BC} } \right)\) và \(\left( {\overrightarrow {AB} ,\overrightarrow {A'C'} } \right)\).

Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó:
a) \(\overrightarrow {AA'} \) và \(\overrightarrow {C'C;} \)
b) \(\overrightarrow {AA'} \) và \(\overrightarrow {BC;} \)
c) \(\overrightarrow {AC} \) và \(\overrightarrow {B'A'} \).
Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho \(SM = 2AM\). Trên cạnh BC, lấy điểm N sao cho \(CN = 2BN\). Chứng minh rằng \(\overrightarrow {MN} = \frac{1}{3}\left( {\overrightarrow {SA} + \overrightarrow {BC} } \right) + \overrightarrow {AB} \).
Cho tứ diện ABCD. Lấy G là trọng tâm của tam giác BCD. Khẳng định nào sau đây là sai?
A. \(\overrightarrow {BG} + \overrightarrow {CG} + \overrightarrow {DG} = \overrightarrow 0 \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
C. \(\overrightarrow {BC} + \overrightarrow {BD} = 3\overrightarrow {BG} \).
D. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
Cho hình hộp ABCD.A’B’C’D’. Lấy M là trung điểm của đoạn thẳng CC’. Vectơ \(\overrightarrow {AM} \) bằng
A. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
B. \(\overrightarrow {AB} + \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AA'} \).
C. \(\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} + \frac{1}{2}\overrightarrow {AA'} \).
D. \(\frac{1}{2}\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào dưới đây là sai?
A. \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AB'} \).
B. \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
C. \(\overrightarrow {AD} + \overrightarrow {BB'} = \overrightarrow {AD'} \).
D. \(\overrightarrow {AB} + \overrightarrow {CC'} = \overrightarrow {AC'} \).
Cho hình hộp ABCD.A’B’C’D’, gọi G là trọng tâm của tam giác BDA’.
a) Biểu diễn \(\overrightarrow {AG} \) theo \(\overrightarrow {AB} ,\overrightarrow {AD} \) và \(\overrightarrow {AA'} \).
b) Từ câu a, hãy chứng tỏ ba điểm A, G và C’ thẳng hàng.
Cho tứ diện ABCD, chứng minh rằng:
a) \(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\);
b) Nếu \(AB \bot CD\) và \(AC \bot BD\) thì \(AD \bot BC\).
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi G là trọng tâm của tam giác BC’D’.
a) Chứng minh rằng \(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\).
b) Tính theo a độ dài đoạn thẳng AG.
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi G là trọng tâm của tam giác BC’D’.
a) Chứng minh rằng \(\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\).
b) Tính theo a độ dài đoạn thẳng AG.
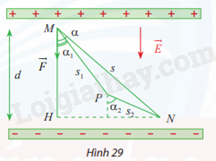
Một lực tĩnh điện \(\overrightarrow F \) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình 29). Biết \(q = {2.10^{ - 12}}C\), vectơ điện trường có độ lớn \(E = 1,{8.10^5}\)N/C và d = MH = 5mm. Tính công A sinh bởi lực tĩnh điện \(\overrightarrow F \).
Phát biểu nào sau đây là đúng?
-
A.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a - \overrightarrow b \)
-
B.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a - k\overrightarrow b \)
-
C.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a - \overrightarrow b ) = k\overrightarrow a \overrightarrow b \)
-
D.
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) bất kì và số thực \(k\), ta có \(k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b \)
Trong không gian cho điểm O và bốn điểm A, B, C, D không thẳng hàng. Điều kiện cần và đủ để A, B, C, D tạo thành hình bình hành là?
-
A.
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
-
B.
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {OD} \)
-
C.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OB} = \overrightarrow {OC} + \frac{1}{2}\overrightarrow {OD} \)
-
D.
\(\overrightarrow {OA} + \frac{1}{2}\overrightarrow {OC} = \overrightarrow {OB} + \frac{1}{2}\overrightarrow {OD} \)
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Xét các vecto \(\overrightarrow x = 2\overrightarrow a - \overrightarrow b \); \(\overrightarrow y = - 4\overrightarrow a + 2\overrightarrow b \); \(\overrightarrow z = - 3\overrightarrow b - 2\overrightarrow c \). Chọn khẳng định đúng?
-
A.
Hai vecto \(\overrightarrow y ,\overrightarrow z \) cùng phương
-
B.
Hai vecto \(\overrightarrow x ,\overrightarrow y \) cùng phương
-
C.
Hai vecto \(\overrightarrow x ,\overrightarrow z \) cùng phương
-
D.
Ba vecto \(\overrightarrow x ,\overrightarrow y ,\overrightarrow z \) đồng phẳng.
Cho hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) có \(AB = a\), \(BC = 2a\), \(A{A_1} = 3a\).
a) \(\left( {\overrightarrow {A{B_1}} ;\overrightarrow {{C_1}D} } \right) = {45^o}\)
b) \(\overrightarrow {{A_1}B} .\overrightarrow {{D_1}D} = 9{a^2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {{C_1}{A_1}} .\overrightarrow {{C_1}{B_1}} \)
d) \(\overrightarrow {{A_1}{D_1}} .\overrightarrow {{C_1}C} = 0\)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O và G là trọng tâm tam giác SBD.
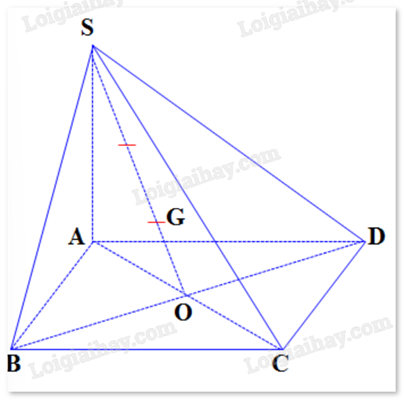
a) \(\overrightarrow {SG} = \frac{2}{3}\overrightarrow {SO} \)
b) \(\overrightarrow {AS} + \overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AG} \)
c) \(\overrightarrow {SA} + \overrightarrow {SC} = 3\overrightarrow {SG} \)
d) \(\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = 12\overrightarrow {GO} \)
Trong các khẳng định sau, khẳng định nào sai?
-
A.
Vecto trong không gian là một đoạn thẳng có hướng
-
B.
Hai vecto cùng phương là hai vecto có giá song song hoặc trùng nhau
-
C.
Hai vecto bằng nhau là hai vecto cùng hướng và có độ dài bằng nhau
-
D.
Hai vecto cùng phương thì cùng hướng
Cho hình hộp ABCD.A’B’C’D’.
a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'} \)
b) \(\overrightarrow {BD} + \overrightarrow {DD'} + \overrightarrow {B'D'} = \overrightarrow {BB'} \)
c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0 \)
d) \(\overrightarrow {AB'} = \overrightarrow {C'D} \)
Cho hình hộp ABCD.A’B’C’D’.
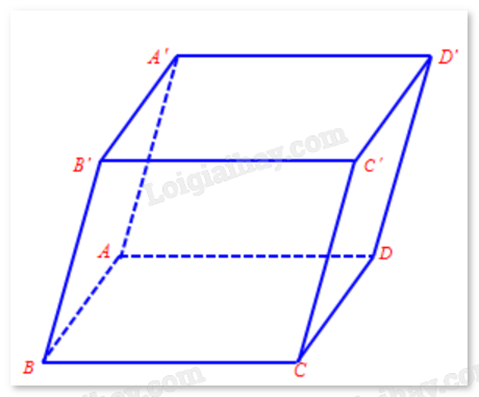
a) \(\overrightarrow {A'A} = - \overrightarrow {CC'} \)
b) \(\overrightarrow {BA'} = \overrightarrow {CD'} \)
c) \(\overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {A'D'} = \overrightarrow {A'C} \)
d) \(\overrightarrow {C'C} + \overrightarrow {AB} + \overrightarrow {B'C'} = 2\overrightarrow {A'C} \)
Cho tứ diện ABCD có AB = AC = AD và \(\widehat {BAC} = \widehat {BAD} = {60^o}\). Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \).
-
A.
\({60^o}\)
-
B.
\({45^o}\)
-
C.
\({120^o}\)
-
D.
\({90^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1\) và \(\overrightarrow a .\overrightarrow b = 3\). Độ dài vecto \(3\overrightarrow a + 5\overrightarrow b \) là?
-
A.
\(5\sqrt 5 \)
-
B.
\(\sqrt {124} \)
-
C.
8
-
D.
124
Cho hình chóp S.ABCD.
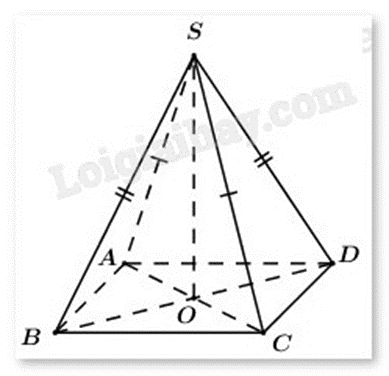
a) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
b) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {CD} \)
c) Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành
d) Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Cho ba vecto \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng. Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Nếu \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) không đồng phẳng thì từ \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) ta suy ra m = n = p = 0
-
B.
Nếu có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \), trong đó \({m^2} + {n^2} + {p^2} > 0\) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
C.
Với ba số thực m, n, p thỏa mãn \(m + n + p \ne 0\) ta có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
-
D.
Nếu giá của \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng quy thì \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng
Cho tứ diện hình chóp S.ABCD có đáy là hình vuông ABCD cạnh bằng a và các cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo góc (MN,SC) bằng
-
A.
\({45^o}\)
-
B.
\({30^o}\)
-
C.
\({90^o}\)
-
D.
\({60^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \ne 0\). Xác định góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\).
-
A.
\(\alpha = {180^o}\)
-
B.
\(\alpha = {0^o}\)
-
C.
\(\alpha = {90^o}\)
-
D.
\(\alpha = {45^o}\)
Cho tứ diện ABCD có các cạnh đều bằng a.
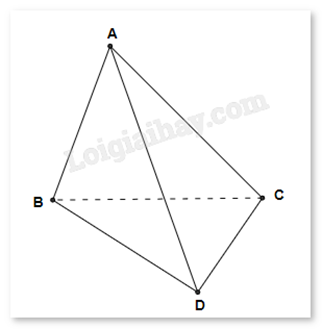
a) \(\overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {BC} + \overrightarrow {DA} = \overrightarrow 0 \)
b) \(\overrightarrow {AB} .\overrightarrow {BC} = - \frac{{{a^2}}}{2}\)
c) \(\overrightarrow {AC} .\overrightarrow {AD} = \overrightarrow {AC} .\overrightarrow {CD} \)
d) \(AB \bot CD\)
Trong các mệnh đề sau, mệnh đề nào sai?
-
A.
Vì I là trung điểm đoạn AB nên từ O bất kì ta có: \(\overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
-
B.
Vì \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \) nên bốn điểm A, B, C, D đồng phẳng
-
C.
Vì \(\overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow 0 \) nên N là trung điểm của đoạn NP
-
D.
Từ hệ thức \(\overrightarrow {AB} = 2\overrightarrow {AC} - 8\overrightarrow {AD} \) ta suy ra ba vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) đồng phẳng
Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vecto \(\overrightarrow {AB} \) và \(\overrightarrow {EG} \)?
-
A.
\({90^o}\)
-
B.
\({60^o}\)
-
C.
\({45^o}\)
-
D.
\({120^o}\)
Cho hai vecto \(\overrightarrow a ,\overrightarrow b \) thỏa mãn \(\left| {\overrightarrow a } \right| = 4\), \(\left| {\overrightarrow b } \right| = 3\), \(\left| {\overrightarrow a - \overrightarrow b } \right| = 4\). Gọi \(\alpha \) là góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \). Chọn khẳng định đúng?
-
A.
\(\cos \alpha = \frac{3}{8}\)
-
B.
\(\alpha = {30^o}\)
-
C.
\(\cos \alpha = \frac{1}{3}\)
-
D.
\(\alpha = {60^o}\)







Danh sách bình luận