Cho tam giác ABC cân tại A và một điểm M tuỳ ý thuộc đoạn thẳng BC. Chứng minh rằng tổng khoảng cách từ điểm M đến đường thẳng AB, AC là một số không đổi
- Xét khi M trùng B, C và khi M khác B, C
- Kẻ \(MP \bot AC;MQ \bot AB\)
-Chứng minh: \(\Delta RBM\) cân tại R
-Chứng minh: MP + MQ = BS + SI = BI = CK.
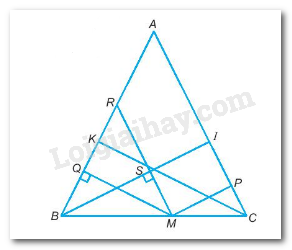
TH1:Khi M trùng với B hay C thì tổng khoảng cách đó là BI hoặc CK
Theo bài 9.8: BI = CK
TH2: Khi M khác B, khác C
Kẻ \(MP \bot AC;MQ \bot AB\)
\( \Rightarrow \)Tổng khoảng cách từ điểm M đến đường thẳng AB, AC là: MQ + MP
Qua M kẻ \(MR // AC\); MR cắt BI tại S.
\( \Rightarrow \widehat C = \widehat {RMB}\) (2 góc đồng vị)
Mà \(\widehat C = \widehat B\)
\( \Rightarrow \widehat B = \widehat {RMB}\)
\( \Rightarrow \Delta RBM\) cân tại R
MQ là khoảng cách từ M đến RB, BS là khoảng cách từ B đến RM
Theo bài 9.8: MQ = BS
Ta có: MR // AC, MP và SI có độ dài là khoảng cách giữa hai đường thẳng đó nên MP = SI
Suy ra: MP + MQ = BS + SI = BI = CK.

Các bài tập cùng chuyên đề
Quan sát Hình 84 và cho biết:
a) Khoảng cách từ điểm O đến đường thẳng a;
b) Khoảng cách từ điểm O đến đường thẳng b;
c) Khoảng cách từ điểm O đến đường thẳng c.

Cho 2 đường thẳng song song c và d. Chứng minh rằng khoảng cách từ mọi điểm thuộc c đến đường thẳng d bằng nhau và bằng khoảng cách từ mọi điểm thuộc đường thẳng d đến đường thẳng c (khoảng cách đó được gọi là khoảng cách giữa hai đường thẳng song song c và d).
Cho 2 điểm phân biệt M, M’ ở cùng phía đối với đường thẳng d (M, M’ không thuộc d). Chứng minh rằng nếu M, M’ có cùng khoảng cách đến đường thẳng d thì MM’ song song với d.
Cho tam giác ABC cân tại A. Chứng minh rằng khoảng cách từ B đến đường thẳng AC bằng khoảng cách từ C đến đường thẳng AB.
Cho góc xOy và điểm B thuộc tia Ox, B ≠ O. Vẽ H là hình chiếu của điểm B trên đường thẳng Oy trong các trường hợp sau:
a) \(\widehat {xOy}\) là góc nhọn;
b) \(\widehat {xOy}\) là góc vuông;
c) \(\widehat {xOy}\) là góc tù.
Cho tam giác ABC vuông cân tại A. Một đường thẳng a đi qua A. Gọi M và N lần lượt là hình chiếu của B và C trên đường thẳng a. Chứng minh:
a) \(\widehat {ABM} = \widehat {CAN}\)
b) CN = MA;
c) Nếu a song song với BC thì MA = AN.
Cho hình vuông ABCD. Hỏi trong bốn đỉnh của hình vuông.
a) Đỉnh nào cách đều hai điểm A và C?
b) Đỉnh nào cách đều hai đường thẳng AB và AD?







Danh sách bình luận